Articles

Henriette-Sophie Lipschütz, Ulrich Reitebuch, Konrad Polthier, and Martin Skrodzki
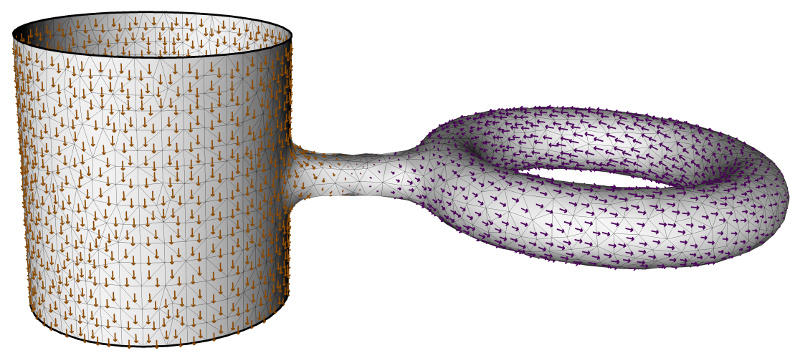
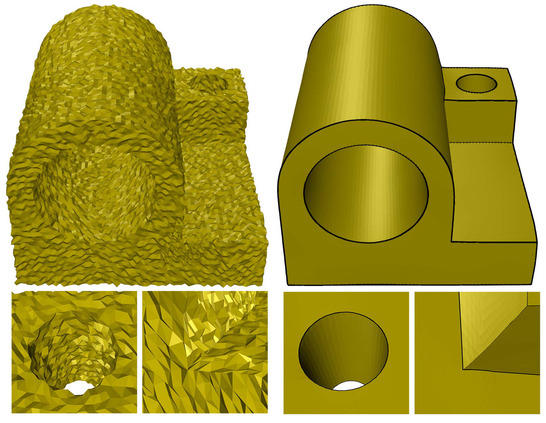
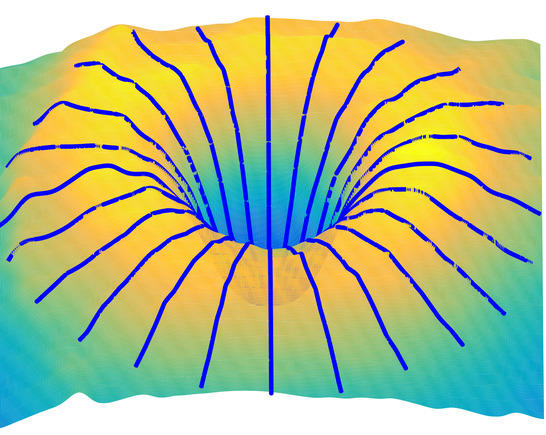
Feature-aware Manifold Meshing and Remeshing of Point Clouds and Polyhedral Surfaces with Guaranteed Smallest Edge Length
In: Computer-Aided Design (2025)
Point clouds and polygonal meshes are widely used when modeling real-world scenarios. Here, point clouds arise, for instance, from acquisition processes applied in various surroundings, such as reverse engineering, rapid prototyping, or cultural preservation. Based on these raw data, polygonal meshes are created to, for example, run various simulations. For such applications, the utilized meshes must be of high quality. This paper presents an algorithm to derive triangle meshes from unstructured point clouds. The occurring edges have a close to uniform length and their lengths are bounded from below. Theoretical results guarantee the output to be manifold, provided suitable input and parameter choices. Further, the paper presents several experiments establishing that the algorithms can compete with widely used competitors in terms of quality of the output and timing and the output is stable under moderate levels of noise. Additionally, we expand the algorithm to detect and respect features on point clouds as well as to remesh polyhedral surfaces, possibly with features. Supplementary material, an extended preprint, a link to a previously published version of the article, utilized models, and implementation details are made available online.
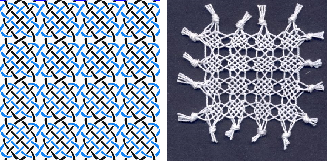
Henriette-Sophie Lipschütz, Ulrich Reitebuch, Konrad Polthier, and Martin Skrodzki
Braidings from Braids and Weavings
In: Proceedings of Bridges 2025: Mathematics and the Arts
We investigate how to replace the threads in a weaving by braided threads and how to interweave them with each other. Based on our findings, we introduce a subdivision scheme applicable to interwoven braids made of an arbitrary number of threads, leading to a fractal-like output. We realize our results both digitally and in handmade form.
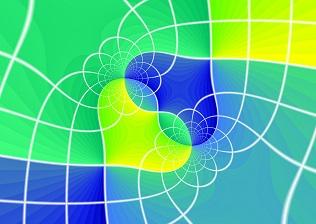
Ulrich Reitebuch, Henriette-Sophie Lipschütz, Konrad Polthier and Martin Skrodzki
Heart of Domain Coloring
In: Proceedings of Bridges 2024: Mathematics, Art, Music, Architecture, Culture
Domain coloring allows for visualization of complex functions. In this paper, we give a brief introduction to domain coloring in general. Then, we investigate its capabilities to create specific shapes, namely hearts. Finally, we present a gallery of our findings.

Henriette Lipschütz, Ulrich Reitebuch, Konrad Polthier, and Martin Skrodzki
Manifold Meshing of Point Clouds with Guaranteed Smallest Edge Length
In: Proceedings of the 2024 International Meshing Roundtable (IMR)
Point clouds and polygonal meshes are widely used when modeling real-world scenarios. Here, point clouds arise, for instance, from acquisition processes applied in various surroundings, such as reverse engineering, rapid prototyping, or cultural preservation. Based on these raw data, polygonal meshes are created to, for example, run various simulations. For such applications, the utilized meshes must be of high quality. This paper presents an algorithm to derive triangle meshes from unstructured point clouds. The occurring edges have a close to uniform length and their lengths are bounded from below. Theoretical results guarantee the output to be manifold, provided suitable input and parameter choices. Further, the paper presents several experiments establishing that the algorithms can compete with widely used competitors in terms of quality of the output and timing. Furthermore, the output is stable under moderate levels of noise.

Ulrich Reitebuch, Henriette Lipschütz, and Konrad Polthier
Visualizing the Kolakoski Sequence
In: Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture
The Kolakoski sequence is a self-generating sequence consisting of 1’s and 2’s only. In addition to the several visualizations of this sequence known, in this paper, a representation is presented illustrating different properties of the Kolakoski sequence and of its generalizations by placing the sequence elements on a spiral.

Ulrich Reitebuch, Martin Skrodzki, Henriette Lipschütz, and Konrad Polthier
Whirling Tiles
In: Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture
Whirling kites, a pattern occurring in Islamic geometric ornaments, is the main inspiration for this paper. First, the pattern is presented as well as different perspectives on how to create it. Then, one of these perspectives is generalized in order to obtain a family of patterns. Finally, we apply the generalization to show these patterns on several tilings.

Henriette Lipschütz, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
Linked Knots from the gyro Operation on the Dodecahedron
In: Proceedings of Bridges 2022: Mathematics, Art, Music, Architecture, Culture
John Horton Conway’s taxonomy for Archimedean and Catalan solids includes the snub and the dual operation, their combination being known as the gyro operation. Intriguingly, recent work showed that the gyro operation can be used to create weaving patterns when applied to planar n-gons. This process can be applied to two-dimensional polyhedral surfaces in R3. In this paper, we investigate the weaving structures that are created on the dodecahedron. We show that the weaving structures can be interpreted via knot theory and written in form of a link diagram. Furthermore, we prove the number of knots arising on the dodecahedron to be six. Finally, we present hand-crafted physical representations of the results in form of balls made of yarn, inspired by Japanese temari.
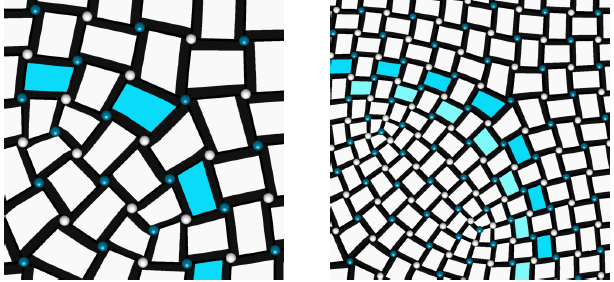
Henriette Lipschütz, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
Weaving patterns inspired by the pentagon snub subdivision scheme
In: Journal of Mathematics and the Arts, Special Issue 'The Art of Illustration'
Various computer simulations regarding, e.g., the weather or structural mechanics, solve complex problems on a two-dimensional domain. They mostly do so by splitting the input domain into a finite set of smaller and simper elements on which the simulation can be run fast and efficiently. This process of splitting can be automatized by using subdivision schemes. Given the wide range of simulation problems to be tackled, an equally wide range of subdivision schemes is available. They create subdivisions that are (mainly) comprised of triangles, quadrilaterals, or hexagons. Furthermore, they ensure that (alost) all vertices have the same number of neighboring vertices. This paper illustrates a subdivions scheme that plits the input domain into pentagons. Repeated application of the scheme gives rise to fractal-like structures. Furthermore, the resulting subdivided domain admits to certain weaving patterns. These patterns are subsequently generalized to several other subdivision schemes. As a final contribution, we provide paper models illustrating the weaving patterns induced by the pentagonal subdivision scheme. Furthermore, we present a jigsaw puzzle illustrating both the subdivision process and the induced weaving pattern. These transform the visual and abstract mathematical algorithms into tactile objects that offer exploration possibilities aside from the visual.

Henriette Lipschütz, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
Single-sized spheres on surfaces (S4)
In: Computer Aided Geometric Design, Volume 85, 2021
Surface representations play a major role in a variety of applications throughout a diverse collection of fields, such as biology, chemistry, physics, or architecture. From a simulation point of view, it is important to simulate the surface as good as possible, including the usage of a wide range of different approximating elements. However, when it comes to manufacturing, it is desirable to have as few different building blocks as possible, as these can then be produced cost-efficiently. Our paper adds a procedure to be used in the simulation of natural phenomena as well as within the designers' creative toolbox. It represents a surface via a collection of equally sized spheres. In the first part of the paper, we give a mathematically precise definition of the underlying problem: How to cover as much as possible of a surface by single-sized spheres. This leads to questions regarding the extremal intersection area of spheres with reasonably well-behaved surfaces, for which we present upper and lower bounds. From these, we deduce how many spheres of a certain, fixed radius can be used at least and at most when interpolating a surface. Following these theoretical results, we compare a depth-first, a breadth-first, and a heuristic algorithm for the generation of surface coverings by single-sized spheres. As opposed to the mathematical description, we show that our algorithms also work for surfaces with boundary elements or sharp features such as edges or corners. We prove the applicability of our algorithm by a multitude of experiments and compare our procedure to ellipsoidal and multi-sized sphere methods.

Martin Skrodzki, Ulrich Reitebuch, and Eric Zimmermann
Experimental visually-guided investigation of sub-structures in three-dimensional Turing-like patterns
In: AUTOMATA2021, 2021
In his 1952 paper “The chemical basis of morphogenesis”, Alan M. Turing presented a model for the formation of skin patterns. While it took several decades, the model has been validated by finding corresponding natural phenomena, e.g. in the skin pattern formation of zebrafish. More surprising, seemingly unrelated pattern formations can also be studied via the model, like e.g. the formation of plant patches around termite hills. In 1984, David A. Young proposed a discretization of Turing’s model, reducing it to an activator/inhibitor process on a discrete domain. From this model, the concept of three-dimensional Turing-like patterns was derived. In this paper, we consider this generalization to pattern-formation in threedimensional space. We are particularly interested in classifying the different arising sub-structures of the patterns. By providing examples for the different structures, we prove a conjecture regarding these structures within the setup of three-dimensional Turing-like pattern. Furthermore, we investigate–guided by visual experiments—how these sub-structures are distributed in the parameter space of the discrete model. We found two-fold versions of zero- and one-dimensional sub-structures as well as two-dimensional sub-structures and use our experimental findings to formulate several conjectures for three-dimensional Turing-like patterns and higherdimensional cases.

Martin Skrodzki and Eric Zimmermann
A Large-Scale Evaluation of Shape-Aware Neighborhood Weights and Neighborhood Sizes
In: Computer-Aided Design, Volume 141, 2021
In this paper, we define and evaluate a weighting scheme for neighborhoods in point sets. Our weighting takes the shape of the geometry, i.e., the normal information, into account. This causes the obtained neighborhoods to be more reliable in the sense that connectivity also depends on the orientation of the point set. We utilize a sigmoid to define the weights based on the normal variation. For an evaluation of the weighting scheme, we turn to a Shannon entropy model for feature classification that can be proven to be non-degenerate for our family of weights. Based on this model, we evaluate our weighting terms on a large scale of both clean and real-world models. This evaluation provides results regarding the choice of optimal parameters within our weighting scheme. Furthermore, the large-scale evaluation also reveals that neighborhood sizes should not be fixed globally when processing models. Finally, we highlight the applicability of our weighting scheme withing the application context of denoising.
Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
Variational shape approximation of point set surfaces
In: Computer Aided Geometric Design, Vol. 80, 2020
In this work, we present a translation of the complete pipeline for variational shape approximation (VSA) to the setting of point sets. First, we describe an explicit example for the theoretically known non-convergence of the currently available VSA approaches. The example motivates us to introduce an alternate version of VSA based on a switch operation for which we prove convergence. Second, we discuss how two operations—split and merge—can be included in a fully automatic pipeline that is in turn independent of the placement and number of initial seeds. Third and finally, we present two approaches how to obtain a simplified mesh from the output of the VSA procedure. This simplification is either based on simple plane intersection or based on a variational optimization problem. Several qualitative and quantitative results prove the relevance of our approach.

Ulrich Reitebuch, Martin Skrodzki, and Konrad Polthier
Discrete Gyroid Surface
In: Proceedings of Bridges 2019: Mathematics, Music, Art, Architecture, Education, Culture, pp. 461-464, 2019
We present a discrete gyroid surface. The gyroid is a triply periodic minimal surface, our discrete version has the same symmetries as the smooth gyroid and can be constructed from simple translational units.

Martin Skrodzki, Ulrike Bath, Kevin Gup, and Konrad Polthier
A Leap Forward: A User Study on Gestural Geometry Exploration
In: Journal of Mathematics and the Arts, Vol. 13, Issue 4, pp. 369-382, 2019
Teaching mathematics in high school and university context often proves hard for both teachers and professors respectively. However, it can be supported by technology. Appliances for 3D digital setups are widely available. They have transcended their intended use as simple in- or output devices and nowadays also play a part in many artistic setups. Thus, they change the way we both perceive and create (digital) models. These changes have to be kept in mind when creating, working with, and presenting 3D art in a digital context.
In this paper, we examine the use of gesture-based controllers in the exploration of mathematical content. A user study was conducted as part of the scientific art and education exhibition “Long Night of Science”. To validate the results, a control group was presented with the same questionnaire and physical models of the mathematical objects (instead of the controller) were used. The participants of the study rated the controllers or the physical models respectively by their individually felt intuitiveness and influence on the perception of the underlying mathematical content. From the data obtained, a connection between the intuitiveness of the controller and a positive influence on the perception of the presented mathematics is shown.
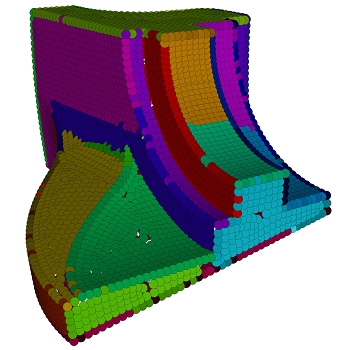
Martin Skrodzki, Eric Zimmermann and Konrad Polthier
Variational Shape Approximation of Point Set Surfaces
In: International Geometry Summit 2019 - Poster Proceedings, pp. 54-57, 2019
This work proposes an algorithm for point set segmentation based on the concept of Variational Shape Approximation (VSA), which uses the k-means approach. It iteratively selects seeds, grows flat planar proxy regions according to normal similarity, and updates the proxies. It is known that this algorithm does not converge in general. We provide a concrete example showing that the utilized error measure can indeed grow during the run of the algorithm. To reach convergence, we propose a modification of the original VSA. Further, we provide two new operations applied to the proxy regions, namely split and merge, which enqueue in the pipeline and act according to a user-given parameter. The advantages over regular VSA are independence of both a prescribed number of proxies and a (manual) selection of seeds. Especially the latter is a common drawback of region-growing approaches in segmentation.

Milena Damrau, Hernán Villamizar and Martin Skrodzki
Eine Datenanalyse der Persistenz und Leistung von Schulkindern im Wettbewerb ”Mathe im Advent“
In: Beiträge zum Mathematikunterricht 2018, pp. 421-424, 2018
"Mathe im Advent" ist ein Wettbewerb, der 2008 von der DMV initiiert wurde. Jedes Jahr im Dezember öffnen Schüler*innen 24 virtuelle Türchen, hinter denen sich mathematische Probleme verstecken - verpackt in kurzen Geschichten über Wichtel. Zu jeder Frage gibt es vier Antworten, von denen genau eine richtig ist. Die Teilnehmer*innen werden dazu aufgefordert, die Aufgaben mit ihren Mitschüler*innen zu besprechen und haben einen Tag Zeit, ihre Lösungen abzugeben. Hochwertige Preise sollen zu guter Leistung motivieren. Auf Grundlage der Daten von mehr als 100.000 Schüler*innen, die 2016 am Wettbewerb teilgenommen haben, untersuchen wir den Einfluss verschiedener Faktoren auf die Leistung und auf die Wahrscheinlichkeit, dass die Schüler*innen möglichst lange am Wettbewerb teilnehmen. Dabei berücksichtigen wir Kriterien auf Basis von Einzel- und Gruppenspiel sowie den Schultyp und bestimmen durch eine Regressionsanalyse und Ereignisszeitanalyse die wichtigsten Aspekte, die zur Leistung und Persistenz beitragen.
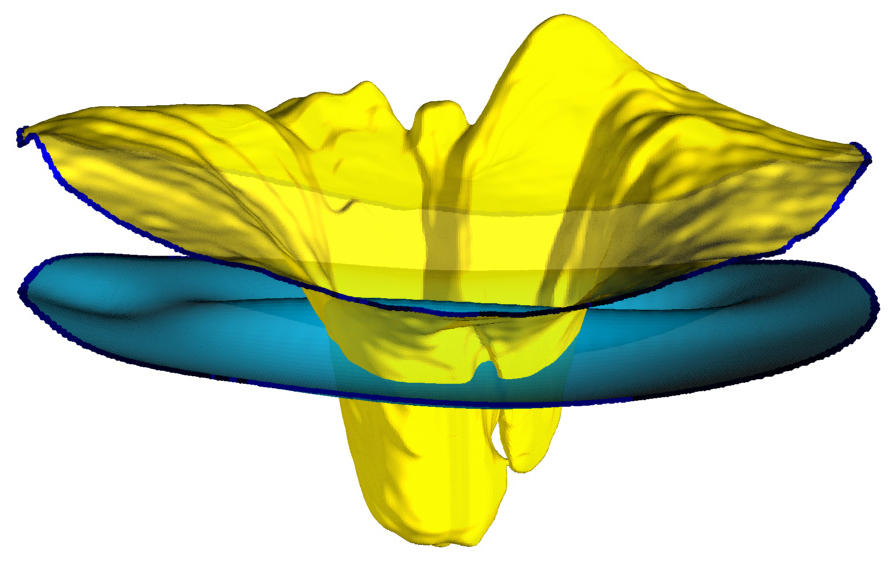
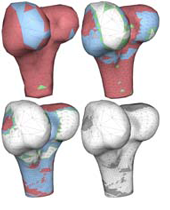
Sunil Kumar Yadav, Ella Maria Kadas, Seyedamirhosein Motamedi, Konrad Polthier, Frank Haußer, Kay Gawlik, Friedemann Paul and Alexander Brandt
Optic nerve head three-dimensional shape analysis
In: Journal of Biomedical Optics, Vol. 23, Issue 10, pp. 1-13, 2018
We present a method for optic nerve head (ONH) 3-D shape analysis from retinal optical coherence tomography (OCT). The possibility to noninvasively acquire in vivo high-resolution 3-D volumes of the ONH using spectral domain OCT drives the need to develop tools that quantify the shape of this structure and extract information for clinical applications. The presented method automatically generates a 3-D ONH model and then allows the computation of several 3-D parameters describing the ONH. The method starts with a high-resolution OCT volume scan as input. From this scan, the model-defining inner limiting membrane (ILM) as inner surface and the retinal pigment epithelium as outer surface are segmented, and the Bruch’s membrane opening (BMO) as the model origin is detected. Based on the generated ONH model by triangulated 3-D surface reconstruction, different parameters (areas, volumes, annular surface ring, minimum distances) of different ONH regions can then be computed. Additionally, the bending energy (roughness) in the BMO region on the ILM surface and 3-D BMO-MRW surface area are computed. We show that our method is reliable and robust across a large variety of ONH topologies (specific to this structure) and present a first clinical application.
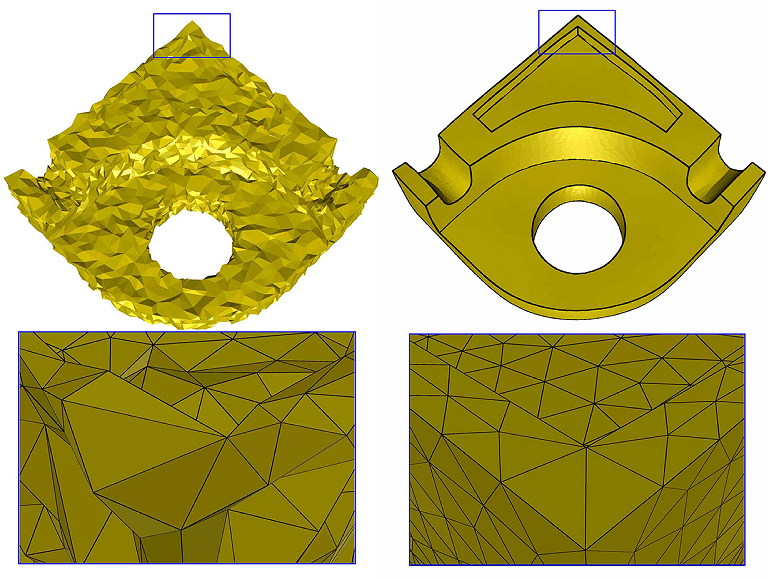
Sunil Kumar Yadav, Ulrich Reitebuch and Konrad Polthier
Robust and High Fidelity Mesh Denoising
In: IEEE Transactions on Visualization and Computer Graphics, Vol. 24, Issue 6, pp. 2304-2310, 2019
This paper presents a simple and effective two-stage mesh denoising algorithm, where in the first stage, face normal filtering is done by using bilateral normal filtering in a robust statistics framework. Tukey's bi-weight function is used as similarity function in the bilateral weighting, which is a robust estimator and stops the diffusion at sharp edges to retain features and removes noise from flat regions effectively. In the second stage, an edge-weighted Laplace operator is introduced to compute a differential coordinate. This differential coordinate helps the algorithm to produce a high-quality mesh without any face normal flips and makes the method robust against high-intensity noise.
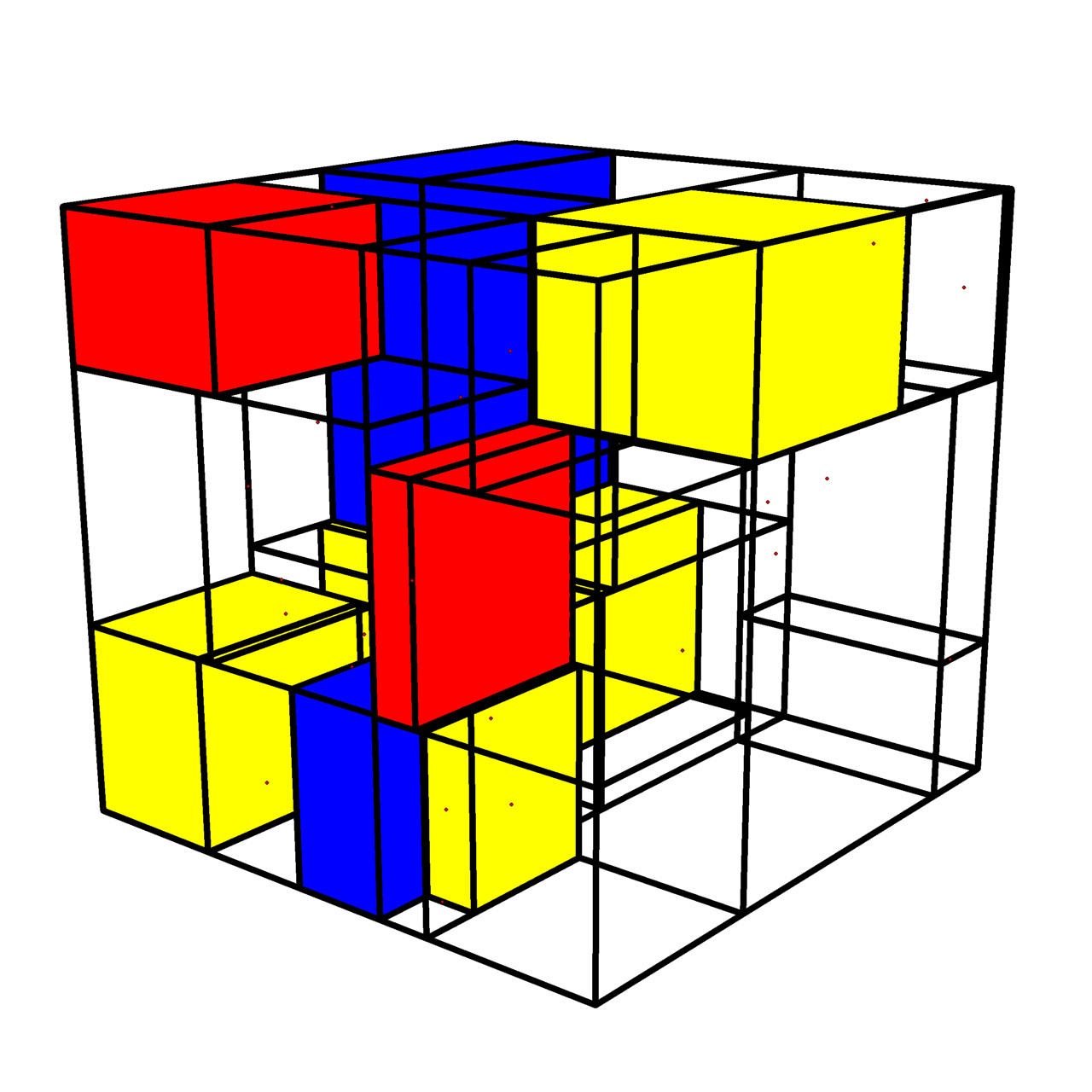
Martin Skrodzki and Konrad Polthier
Mondrian Revisited: A Peek Into The Third Dimension
In: Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, pp. 99-106, 2018
The artist Piet Mondrian (1872 – 1944) is most famous for his abstract works utilizing primary colors and axes-parallel black lines. A similar structure can be found in visualizations of the KdTree data structure used in computational geometry for range searches and neighborhood queries. In this paper, we systematically explore these visualizations and their connections to Mondrian’s work and give a dimension-independent generalization of Mondrian-like pieces.

Ulrich Reitebuch, Henriette Lipschütz and Konrad Polthier
Girih Tiles in 3D
In: Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, 511-514, 2018
In Islamic architecture and art, girih patterns are used for decorations of buildings such as mosques or palaces. Based on the construction of 2D girih patterns, we provide a corresponding procedure to construct 3D girih patterns covering R³ completely.

Ulrich Reitebuch, Eric Zimmermann and Konrad Polthier
Two-Layer Woven Surfaces with Planar Faces
In: Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, 147-154, 2018
We create two-layer interwoven surfaces with (a) planar faces from (b) arbitrary input meshes such that these can be built from cardboard or any other planar material. There are pre-existing constructions for symmetric and regular meshes but these are lacking one or both of the before mentioned attributes (a), (b). We want to emphasize that there do not exist solutions for edge-interpolating or barycentric-apex-created two-layer weavings in general. Hence, we propose constructions in terms of approximations, missing one of the conditions (a), (b) alone, but not both.
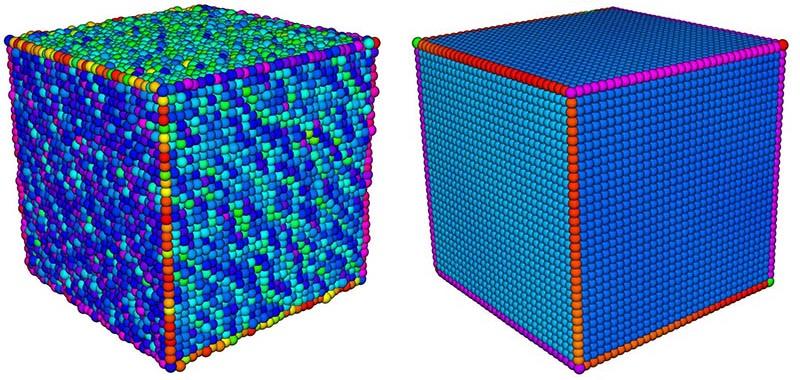
Sunil Kumar Yadav, Ulrich Reitebuch, Martin Skrodzki, Eric Zimmermann and Konrad Polthier
Constraint-based point set denoising using normal voting tensor and restricted quadratic error metrics
In: Computers & Graphics, Vol. 74, pp. 234-243, 2018
In many applications, point set surfaces are acquired by 3D scanners. During this acquisition process, noise and outliers are inevitable. For a high fidelity surface reconstruction from a noisy point set, a feature preserving point set denoising operation has to be performed to remove noise and outliers from the input point set. To suppress these undesired components while preserving features, we introduce an anisotropic point set denoising algorithm in the normal voting tensor framework. The proposed method consists of three different stages that are iteratively applied to the input: in the first stage, noisy vertex normals, are initially computed using principal component analysis, are processed using a vertex-based normal voting tensor and binary eigenvalues optimization. In the second stage, feature points are categorized into corners, edges, and surface patches using a weighted covariance matrix, which is computed based on the processed vertex normals. In the last stage, vertex positions are updated according to the processed vertex normals using restricted quadratic error metrics. For the vertex updates, we add different constraints to the quadratic error metric based on feature (edges and corners) and non-feature (planar) vertices. Finally, we show our method to be robust and comparable to state-of-the-art methods in several experiments.
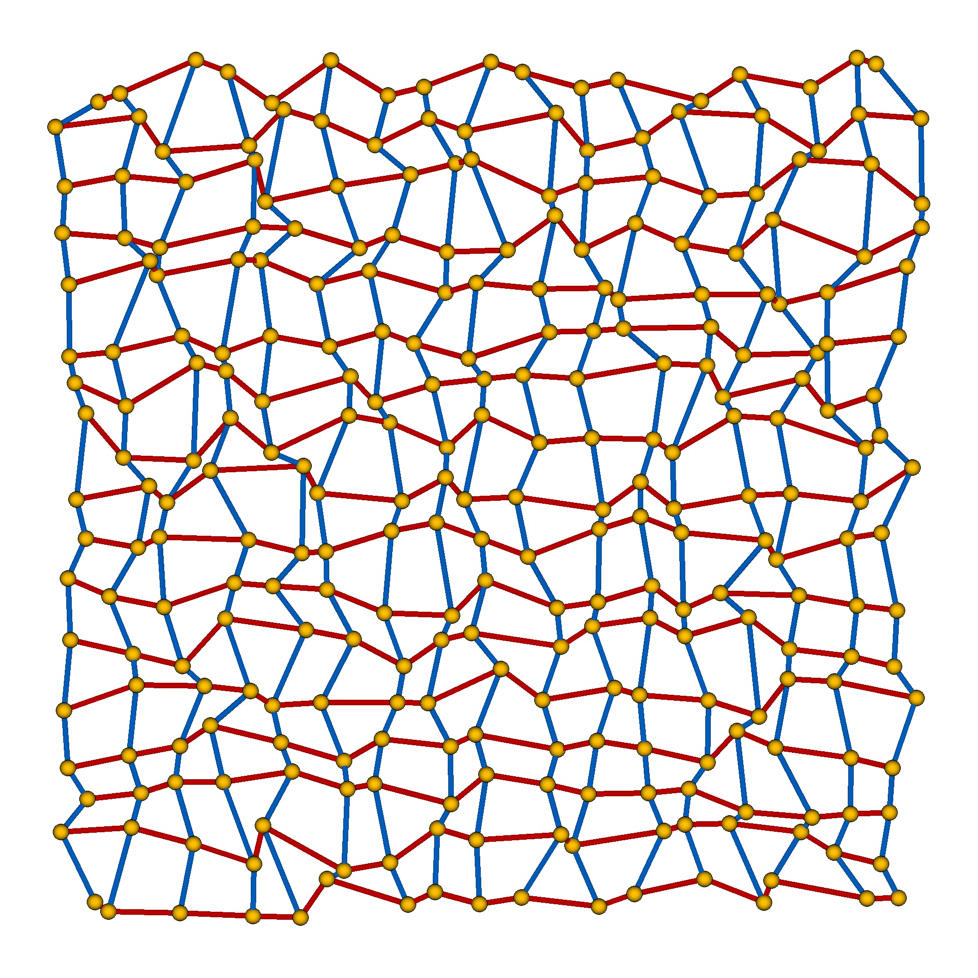
Martin Skrodzki, Ulrich Reitebuch, Konrad Polthier and Shagnik Das
Combinatorial and Asymptotical Results on the Neighborhood Grid Data Structure
In: Proceedings of EuroCG 2018
In 2009, Joselli et al. introduced the Neighborhood Grid data structure for fast computation of neighborhood estimates in point sets. Even though the data structure has been used in several applications and shown to be practically relevant, it is theoretically not yet well understood. The purpose of this paper is to give results on the complexity of building algorithms – both singlecore and parallel – for the neighborhood grid. Furthermore, current investigations on related combinatorial questions are presented.

Martin Skrodzki, Johanna Jansen and Konrad Polthier
Directional Density Measure To Intrinsically Estimate And Counteract Non-Uniformity In Point Clouds
In: Computer Aided Geometric Design, Issue 64, pp. 73-89, 2018
With the emergence of affordable 3D scanning and printing devices, processing of large point clouds has to be performed in many applications. Several algorithms are available for surface reconstruction, smoothing, and parametrization. However, many of these require the sampling of the point cloud to be uniform or at least to be within certain controlled parameters. For nonuniformly sampled point clouds, some methods have been proposed that deal with the nonuniformity by adding additional information such as topological or hierarchical data. In this paper, we focus on point clouds sampling surfaces in R3. We present the notion of local directional density measure that can be intrinsically computed within the point cloud, that is without further knowledge of the geometry despite the given point samples. Specifically, we build on the work of [1] to derive a local, directed, and discrete measure for density. Furthermore, we derive another discrete and a smooth density measure and compare these three experimentally. Each of the three considered measures gives density weights to use in discretizations of operators such that these become independent of sampling uniformity. We demonstrate the effectiveness of our method on both synthetic and real world data.
Sunil Kumar Yadav, Ulrich Reitebuch and Konrad Polthier
Mesh Denoising based on Normal Voting Tensor and Binary Optimization
In: IEEE Transactions on Visualization and Computer Graphics, Vol. 24, Issue 8, pp. 2366-2379, 2018
This paper presents a two-stage mesh denoising algorithm. Unlike other traditional averaging approaches, our approach uses an element-based normal voting tensor to compute smooth surfaces. By introducing a binary optimization on the proposed tensor together with a local binary neighborhood concept, our algorithm better retains sharp features and produces smoother umbilical regions than previous approaches. On top of that, we provide a stochastic analysis on the different kinds of noise based on the average edge length. The quantitative results demonstrate that the performance of our method is better compared to state-of-the-art smoothing approaches.
Sunil Kumar Yadav, Seyedamirhosein Motamedi, Timm Oberwahrenbrock, Frederike Cosima Oertel, Konrad Polthier, Friedemann Paul, Ella Maria Kadas, and Alexander U. Brandt
CuBe: parametric modeling of 3D foveal shape using cubic Bézier
In: Biomedical Optics Express, Vol. 8, Issue 9, pp. 4181-4199, 2017
Optical coherence tomography (OCT) allows three-dimensional (3D) imaging of the retina, and is commonly used for assessing pathological changes of fovea and macula in many diseases. Many neuroinflammatory conditions are known to cause modifications to the fovea shape. In this paper, we propose a method for parametric modeling of the foveal shape. Our method exploits invariant features of the macula from OCT data and applies a cubic Bézier polynomial along with a least square optimization to produce a best fit parametric model of the fovea. Additionally, we provide several parameters of the foveal shape based on the proposed 3D parametric modeling. Our quantitative and visual results show that the proposed model is not only able to reconstruct important features from the foveal shape, but also produces less error compared to the state-of-the-art methods. Finally, we apply the model in a comparison of healthy control eyes and eyes from patients with neuroinflammatory central nervous system disorders and optic neuritis, and show that several derived model parameters show significant differences between the two groups.

Martin Skrodzki and Konrad Polthier,
Turing-Like Patterns Revisited: A Peek Into The Third Dimension
In: Proceedings of Bridges 2017: Mathematics, Art, Music, Architecture, Education, Culture, pp. 415-418, 2017
Beginning with their introduction in 1952 by Alan Turing, Turing-like patterns have inspired research in several different fields. One of these is the field of cellular automata, which have been utilized to create Turing-like patterns by David A. Young and others. In this paper we provide a generalization of these patterns to the third dimension. Several visualizations are given to illustrate the created models.

Faniry Razafindrazaka and Konrad Polthier,
Optimal Base Complexes for Quadrilateral Meshes
In: Computer Aided Geometric Design, pp. 63-74, 2017
In this paper we give an explicit algorithm to optimize the global structure of quadrilateral meshes i.e base complexes, using a graph perfect matching. The approach consists of constructing a special graph over the singularity set of the mesh and finding all quadrilateral based complex subgraphs of that graph. We show by construction that there is always an optimal base complex to a given quadrilateral mesh relative to coarseness versus geometry awareness. Local structures of the mesh induce extra constraints which have been previously ignored but can give a completely different layout. These are diagonal, multiple and close to zero length edges. We give an efficient solution to solve these problems and improve the computation speed. Generally all base complex optimization schemes are bounded by the topology of the singularities, we explore the space of layouts encoded in the graph to identify removable singularities of the mesh while simultaneously optimize the base complex.
[pdf, 15 MB][BibTex]
Konstantin Poelke and Konrad Polthier
Discrete Topology-Revealing Vector Fields on Simplicial Surfaces with Boundary
To appear in: TopoInVis 2017 proceedings
We present a discrete Hodge-Morrey-Friedrichs decomposition for piecewise constant vector fields on simplicial surfaces with boundary which is structurally consistent with the smooth theory. In particular, it preserves a deep linkage between metric properties of the spaces of harmonic Dirichlet and Neumann fields and the topology of the underlying geometry, which reveals itself as a discrete de Rham theorem and a certain angle between Dirichlet and Neumann fields. We illustrate and discuss this linkage on several geometries.
[Extended Abstract, pdf, 1 MB][Article][BibTex]

Martin Skrodzki, Ulrich Reitebuch and Konrad Polthier,
Chladni Figures Revisited: A Peek Into The Third Dimension
In: Proceedings of Bridges, pp. 481-484, 2016
In his 1802 book ”Acoustics”, Ernst Florens Friedrich Chladni describes how to visualize different vibration modes using sand, a metal plate, and a violin bow. We will review the underlying physical and mathematical formulations and lift them to the third dimension. Finally, we present some of the resulting three dimensional Chladni figures.
Konstantin Poelke and Konrad Polthier,
Boundary-aware Hodge decompositions for piecewise constant vector fields
In: Computer-Aided Design, Vol. 78, pp. 126-136, 2016
1st price at SPM 2016 best paper awards
We provide a theoretical framework for discrete Hodge-type decomposition theorems of piecewise constant vector fields on simplicial surfaces with boundary that is structurally consistent with decomposition results for differential forms on smooth manifolds with boundary. In particular, we obtain a discrete Hodge–Morrey–Friedrichs decomposition with subspaces of discrete harmonic Neumann fields and Dirichlet fields, which are representatives of absolute and relative cohomology and therefore directly linked to the underlying topology of the surface. In addition, we discretize a recent result that provides a further refinement of the spaces of discrete harmonic Neumann and Dirichlet fields, and answer the question in which case one can hope for a complete orthogonal decomposition involving both spaces at the same time. As applications, we present a simple strategy based on iterated L2-projections to compute refined Hodge-type decompositions of vector fields on surfaces according to our results, which give a more detailed insight than previous decompositions. As a proof of concept, we explicitly compute harmonic basis fields for the various significant subspaces and provide exemplary decompositions for two synthetic vector fields.
[Article] [Preprint pdf, 6 MB][BibTex]
Anna Wawrzinek and Konrad Polthier,
Integration of generalized B-spline functions on Catmull–Clark surfaces at singularities
In: Computer-Aided Design, Vol. 78, pp. 60-70, 2016
Subdivision surfaces are a common tool in geometric modeling, especially in computer graphics and computer animation. Nowadays, this concept has become established in engineering too. The focus here is on quadrilateral control grids and generalized B-spline surfaces of Catmull–Clark subdivision type. In the classical theory, a subdivision surface is defined as the limit of the repetitive application of subdivision rules to the control grid. Based on Stam′s idea, the labour-intensive process can be avoided by using a natural parameterization of the limit surface. However, the simplification is not free of defects. At singularities, the smoothness of the classically defined limit surface has been lost. This paper describes how to rescue the parameterization by using a subdivision basis function that is consistent with the classical definition, but is expensive to compute. Based on this, we introduce a characteristic subdivision finite element and use it to discretize integrals on subdivision surfaces. We show that in the integral representation the complicated parameterization reduces to a decisive factor. We compare the natural and the characteristic subdivision finite element approach solving PDEs on surfaces. As model problem we consider the mean curvature flow, whereby the computation is done on the step-by-step changing geometry.
Konrad Polthier, Faniry Razafindrazaka
Discrete Geometry for Reliable Surface Quad-Remeshing.
In: Applications + Practical Conceptualization + Mathematics = fruitful Innovation, Proceedings of the Forum of Mathematics for Industry 2014. Springer. 2014
In this overview paper we will glimpse how new concepts from discrete differential geometry help to provide a unifying vertical path through parts of the geometry processing pipeline towards a more reliable interaction. As an example, we will introduce some concepts from discrete differential geometry and the QuadCover algorithm for quadrilateral surface parametrization. QuadCover uses exact discrete differential geometric concepts to convert a pair (simplicial surface, guiding frame field) to a global quad-parametrization of the unstructured surface mesh. Reliability and robustness is an omnipresent issue in geometry processing and computer aided geometric design since its beginning. For example, the variety of incompatible data structures for geometric shapes severely limits a reliable exchange of geometric shapes among different CAD systems as well as a unifying mathematical theory. Here the integrable nature of the discrete differential geometric theory and its presented application to an effective remeshing algorithm may serve an example to envision an increased reliability along the geometry processing pipeline through a consistent processing theory.
[preprint pdf, 10.7 MB] [BibTex]
Sebastian Götschel, Christoph von Tycowicz, Konrad Polthier, Martin Weiser
Reducing Memory Requirements in Scientific Computing and Optimal Control.
In: Multiple Shooting and Time Domain Decomposition Methods. Springer. 2015
This paper introduces a new approach to automatically generate pure quadrilateral patch layouts on manifold meshes. The algorithm is based on a careful construction of a singularity graph of a given input frame field or a given periodic global parameterization. A pure quadrilateral patch layout is then derived as a constrained minimum weight perfect matching of that graph. The resulting layout is optimal relative to a balance between coarseness and geometric feature alignment. We formulate the problem of finding pure quadrilateral patch layouts as a global optimization problem related to a well-known concept in graph theory. The main advantage of the new method is its simplicity and its computation speed. Patch layouts generated by the present algorithm are high quality and are very competitive compared to current state of the art.
[preprint pdf, 828 KB] [BibTex]
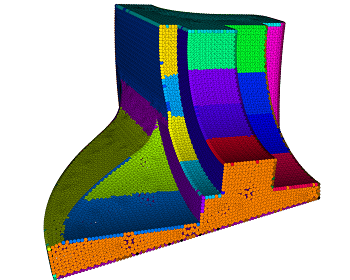
Faniry Razafindrazaka, Ulrich Reitebuch, Konrad Polthier
Perfect Matching Quad Layouts for Manifold Meshes.
Symposium on Geometry Processing (SGP), Graz 2015
This paper introduces a new approach to automatically generate pure quadrilateral patch layouts on manifold meshes. The algorithm is based on a careful construction of a singularity graph of a given input frame field or a given periodic global parameterization. A pure quadrilateral patch layout is then derived as a constrained minimum weight perfect matching of that graph. The resulting layout is optimal relative to a balance between coarseness and geometric feature alignment. We formulate the problem of finding pure quadrilateral patch layouts as a global optimization problem related to a well-known concept in graph theory. The main advantage of the new method is its simplicity and its computation speed. Patch layouts generated by the present algorithm are high quality and are very competitive compared to current state of the art.
[preprint pdf, 0.5 MB] [BibTex]
Faniry Razafindrazaka, Konrad Polthier
Realization of Regular Maps of Large Genus.
In: Topological and Statistical Methods for Complex Data. Mathematics and Visualization series. Pages 239-252. Springer. 2015
Tiling of closed surfaces into non-overlapping faces is one of the central topics in surface topology and computer graphics. Either the surface is given and a nice tiling of this surface has to be found or the tiling is given and the surface on which this tiling is the most symmetric has to be found. This paper explores the later case but restricts the tiling scheme to the class of regular maps.
[pdf, 11.7 MB] [BibTex]

Christian Schulz, Christoph von Tycowicz, Hans-Peter Seidel, and Klaus Hildebrandt
Animating Deformable Objects using Sparse Spacetime Constraints.
In: ACM Transactions on Graphics (SIGGRAPH 2014), Volume 33, Issue 4, July 2014, pages 109:1-109:10.
We propose a scheme for animating deformable objects based on spacetime optimization. The main feature is that it robustly and quickly (within a few seconds) generates interesting motion from a sparse set of spacetime constraints. Providing only partial (as opposed to full) keyframes for positions and velocities is sufficient. The computed motion satisfies the constraints and the remaining degrees of freedom are determined by physical principles using elasticity and the spacetime constraints paradigm. Our modeling of the spacetime optimization problem combines dimensional reduction, modal coordinates, wiggly splines, and rotation strain warping. Controlling the warped motion requires the derivative of the warp map. We derive a representation of the derivative that can be efficiently and robustly evaluated. Our solver is based on a theorem that characterizes the solutions of the optimization problem and allows us to restrict the optimization to very low-dimensional search spaces. This treatment of the optimization problem avoids a time discretization and the resulting method can robustly deal with sparse input and wiggly motion.
[pdf, 8.5 MB] [BibTex]

Konrad Polthier, John M. Sullivan, Günter M. Ziegler, Hans-Christian Hege
Visualization.
In: MATHEON-Mathematics for Key Technology. EMS Series in Industrial and Applied Mathematics 1. European Mathematical Society 2014. Page 335-339
[pdf, 1.9 MB] [BibTex]
Konrad Polthier, Alexander Bobenko, Klaus Hildebrandt, Ralf Kornhuber, Christoph von Tycowicz, Harry Yserentant, Günter M. Ziegler
Geometry Processing.
In: MATHEON-Mathematics for Key Technology. EMS Series in Industrial and Applied Mathematics 1. European Mathematical Society 2014. Page 341-355
[pdf, 6.35 MB] [BibTex]
Felix Kälberer, Matthias Nieser, Konrad Polthier
Showcase 22, Mathematics in Hollywood.
In: MATHEON-Mathematics for Key Technology. EMS Series in Industrial and Applied Mathematics 1. European Mathematical Society 2014. Page 356-357
[pdf, 717 KB] [BibTex]
John M. Sullivan, Ulrich Pinkall, Konrad Polthier
Mathematical Visualization, in: MATHEON-Mathematics for Key Technology. EMS Series in Industrial and Applied Mathematics 1. European Mathematical Society 2014. Page 381-392
[pdf, 12.7 MB] [BibTex]
Konstantin Poelke, Zoi Tokoutsi, Konrad Polthier
Complex Polynomial Mandalas and their Symmetries.
In: Proceedings of Bridges 2014, Tessellations Publishing, Page 433-436
We present an application of the classical Schwarz reflection principle to create complex mandalas—symmetric shapes resulting from the transformation of simple curves by complex polynomials—and give various illustrations of how their symmetry relates to the polynomials' set of zeros. Finally we use the winding numbers inside the segments enclosed by the transformed curves to obtain fully coloured patterns in the spirit of many mandalas found in real-life.
[pdf, 4.5 MB] [BibTex]
Faniry Razafindrazaka, Konrad Polthier
Regular Surfaces and Regular Maps.
In: Proceedings of Bridges 2014, Tessellations Publishing, Page 225-234
A regular surface is a closed genusgsurface defined as the tubular neighbourhood of the edge graph of a regularmap. A regular map is a family of disc type polygons glued together to form a 2-manifold which is flag transitive.The visualization of this highly symmetric surface is an intriguing and challenging problem. Unlike regular maps,regular surfaces can always be visualized as 3D embeddings. In this paper, we introduce an algorithm to visualize theregular surface formed around the tubular neighborhood of a regular map. Our algorithm takes as input the symmetrygroup of a regular map and outputs a 3D realization of its regular surface. This surface can be interactively modifiedand used as a target shape for other regular maps. As a result, we find new realizations of regular maps ranging fromgenus 9 to 85.
[pdf, 1.5 MB] [BibTex]
Niklas Krauth, Matthias Nieser, Konrad Polthier
Differential-Based Geometry and Texture Editing with Brushes
In: Journal of Mathematical Imaging and Vision, Volume 48, Issue 2 (2014), Page 359-368
We present an interactive modeling framework for 3D shapes and for texture maps. The technique combines a differential-based deformation method with the idea of geometry brushes that allow to interactively apply modifications by painting on the geometry. Whereas most other deformation techniques demand the designer to define and move hard constrained regions on the surface, the proposed modeling process is similar to sculpting. Geometry brushes allow the user to locally manipulate the metric, enlarge, shrink or rotate parts of the surface and to generate bumps. In a similar way it is possible to modify texture maps, or more generally, arbitrary tensor maps on surfaces. The local modifications of the surface are integrated to a globally consistent deformation and visualized in real-time. While the geometry brushes are intended for local editing, the underlying technique can also be applied globally. We show how differentials may be modified for creating specific effects, like cartoonization of shapes or adjusting texture images.
[preprint pdf, 10.4 MB] [supplementary video] [BibTex]
Eduardo Colli, Fidel R. Nemenzo, Konrad Polthier, Christiane Rousseau
Mathematics is everywhere
In: Proceedings of the International Congress of Mathematicians. Pages 799-811.
Mathematics is everywhere" is the title for a panel at ICM 2014. The four panelists discuss what can be put under this title, what are the messages that can be passed to the public, and how to pass these messages. To most mathematicians, it seems obvious that mathematics is everywhere, and a living discipline within science and technology. Yet, how many of them are able to convey the message? And, when most people look around, they do not see mathematics, they do not know about the mathematics underlying the technology, they know very little about the role of mathematics in the scientifc venture. Can we help building a powerful message? Can we unite forces for better passing it?
[pdf, 1.64 MB] [BibTex]

Faniry Razafindrazaka, Konrad Polthier
The 6-ring
In: Bridges 2013, July 27-31, Enschede.
The 6-ring is a tubular surface of genus 13, obtained by gluing together twenty-four 12-gons which follows the regularity of the map R13.2′{12,3}. It is constructed from six rings of two Borromean rings, has the twenty-four elements of an oriented cube and matches nicely with the 6-coloring of R13.2′{12,3}. The 6-ring has minimal twists and geometrically equivalent sets of four 12-gons. We explicitly construct this highly symmetric surface from two Borromean rings together with a detailed mapping of the 12-gons.
[pdf, 2.24 MB] [BibTex]
Faniry Razafindrazaka, Konrad Polthier
Regular map smoothing
In: DGCI 2013, March 20-22, Seville.
A regular map is a family of equivalent polygons, glued together to form a closed surface without boundaries which is vertex, edge and face transitive. The commonly known regular maps are derived from the Platonic solids and some tessellations of the torus. There are also regular maps of genus greater than 1 which are traditionally viewed as finitely generated groups. RMS (Regular Map Smoothing) is a tool for visualizing a geometrical realization of such a group either as a cut-out in the hyperbolic space or as a compact surface in 3−space. It provides also a tool to make the resulting regular map more appealing than before. RMS achieves that by the use of a coloring scheme based on coset enumeration, a Catmull-Clark smoothing scheme and a force-directed algorithm with topology preservation.
[pdf, 0.3 MB] [BibTex]

Christoph von Tycowicz, Christian Schulz, Hans-Peter Seidel, Klaus Hildebrandt
An Efficient Construction of Reduced Deformable Objects
In: ACM Transactions on Graphics (SIGGRAPH Asia 2013), Volume 32, Issue 6.
Many efficient computational methods for physical simulation are based on model reduction. We propose new model reduction techniques for the approximation of reduced forces and for the construction of reduced shape spaces of deformable objects that accelerate the construction of a reduced dynamical system, increase the accuracy of the approximation, and simplify the implementation of model reduction. Based on the techniques, we introduce schemes for real-time simulation of deformable objects and interactive deformation-based editing of triangle or tet meshes. We demonstrate the effectiveness of the new techniques in different experiments with elastic solids and shells and compare them to alternative approaches.
[preprint pdf, 11 MB] [supplementary video] [DOI] [BibTex]

Esfandiar Nava-Yazdani, Konrad Polthier
De Casteljauʼs algorithm on manifolds
In: Computer Aided Geometric Design, Volume 30, Issue 7, October 2013, Pages 722-732
This paper proposes a generalization of the ordinary de Casteljau algorithm to manifold-valued data including an important special case which uses the exponential map of a symmetric space or Riemannian manifold. We investigate some basic properties of the corresponding Bézier curves and present applications to curve design on polyhedra and implicit surfaces as well as motion of rigid body and positive definite matrices. Moreover, we apply our approach to construct canal and developable surfaces.
Klaus Hildebrandt, Konrad Polthier
Consistent discretizations of the Laplace–Beltrami operator and the Willmore energy of surfaces
In: Oberwolfach Reports, Workshop 1228: Discrete Differential Geometry, 2012.
A fundamental aspect when translating classical concepts from smooth differential geometry, such as differential operators or geometric functionals, to corresponding discrete notions is consistency. Here, we are concerned with the construction of consistent discrete counterparts to the Laplace–Beltrami operator and the Willmore energy on polyhedral surfaces.
[BibTex]

Konstantin Poelke, Konrad Polthier
Domain Coloring of Complex Functions: An Implementation-Oriented Introduction
In: IEEE Computer Graphics and Applications, vol. 32, no. 5, pp. 90-97, Sept.-Oct., 2012
This article gives a short overview of domain coloring for complex functions that have four-dimensional function graphs and therefore can't be visualized traditionally. The authors discuss several color schemes, focus on various aspects of complex functions, and provide Java-like pseudocode examples explaining the crucial ideas of the coloring algorithms to allow for easy reproduction.
[preprint pdf, 1,2 MB] [DOI] [BibTex]

Ulrich Bauer, Carsten Lange, Max Wardetzky
Optimal topological simplification of discrete functions on surfaces
In: Discrete and Computational Geometry 47 (2012), pp 347-377.
We present an efficient algorithm for computing a function that minimizes the number of critical points among all functions within a prescribed distance $\delta$ from a given input function. The result is achieved by establishing a connection between discrete Morse theory and persistent homology. Our method completely removes homological noise with persistence less than $2\delta$, constructively proving that the lower bound on the number of critical points given by the stability theorem of persistent homology is tight in dimension two for any input function.
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Interactive spacetime control of deformable objects
In: ACM Transactions on Graphics 31(4) (SIGGRAPH 2012) Article No. 71.
Creating motions of objects or characters that are physically plausible and follow an animator's intent is a key task in computer animation. The spacetime constraints paradigm is a valuable approach to this problem, but it suffers from high computational costs. Based on spacetime constraints, we propose a framework for controlling the motion of deformable objects that offers interactive response times. This is achieved by a model reduction of the underlying variational problem, which combines dimension reduction, multipoint linearization, and decoupling of ODEs. After a preprocess, the cost for creating or editing a motion is reduced to solving a number of one-dimensional spacetime problems, whose solutions are the wiggly splines introduced by Kass and Anderson [2008]. We achieve interactive response times through a new fast and robust numerical scheme for solving the one-dimensional problems that is based on a closed-form representation of the wiggly splines.
[preprint pdf, 3.7 MB] [supplementary video, 76 MB] [DOI] [BibTex]

Hao Pan, Yi-King Choi, Yang Liu, Wenchao Hu, Qiang Du, Konrad Polthier, Caiming Zhang, Wenping Wang
Robust Modeling of Constant Mean Curvature Surfaces
In: ACM Transactions on Graphics 31(4) (SIGGRAPH 2012) Article No. 85.
We present a new method for modeling discrete constant mean curvature (CMC) surfaces, which arise frequently in nature and are highly demanded in architecture and other engineering applications. Our method is based on a novel use of the CVT (centroidal Voronoi tessellation) optimization framework. We devise a CVT-CMC energy function defined as a combination of an extended CVT energy and a volume functional. We show that minimizing the CVT-CMC energy is asymptotically equivalent to minimizing mesh surface area with a fixed volume, thus defining a discrete CMC surface. The CVT term in the energy function ensures high mesh quality throughout the evolution of a CMC surface in an interactive design process for form finding. Our method is capable of modeling CMC surfaces with fixed or free boundaries and is robust with respect to input mesh quality and topology changes. Experiments show that the new method generates discrete CMC surfaces of improved mesh quality over existing methods
[preprint pdf, 1.4 MB] [DOI] [BibTex]

Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Interactive Surface Modeling using Modal Analysis
In: ACM Transactions on Graphics, Volume 30, Issue 5, October 2011, pages 119:1-119:11. Will be presented at SIGGRAPH 2012.
We propose a framework for deformation-based surface modeling that is interactive, robust and intuitive to use. The deformations are described by a non-linear optimization problem that models static states of elastic shapes under external forces which implement the user input. Interactive response is achieved by a combination of model reduction, a robust energy approximation, and an efficient quasi-Newton solver. Motivated by the observation that a typical modeling session requires only a fraction of the full shape space of the underlying model, we use second and third derivatives of a deformation energy to construct a low-dimensional shape space that forms the feasible set for the optimization. Based on mesh coarsening, we propose an energy approximation scheme with adjustable approximation quality. The quasi-Newton solver guarantees superlinear convergence without the need of costly Hessian evaluations during modeling. We demonstrate the effectiveness of the approach on different examples including the test suite introduced in [Botsch and Sorkine 2008].
[low-res pdf, 2.0 MB, high-res pdf, 15 MB] [video, 57 MB] [DOI] [BibTex]
Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Modal Shape Analysis beyond Laplacian
In: Computer Aided Geometric Design, Volume 29, Issue 5, June 2012, Pages 204–218.
In recent years, substantial progress in shape analysis has been achieved through methods that use the spectra and eigenfunctions of discrete Laplace operators. In this work, we study spectra and eigenfunctions of discrete differential operators that can serve as an alternative to the discrete Laplacians for applications in shape analysis. We construct such operators as the Hessians of surface energies, which operate on a function space on the surface, or of deformation energies, which operate on a shape space. In particular, we design a quadratic energy such that, on the one hand, its Hessian equals the Laplace operator if the surface is a part of the Euclidean plane, and, on the other hand, the Hessian eigenfunctions are sensitive to the extrinsic curvature (e.g. sharp bends) on curved surfaces. Furthermore, we consider eigenvibrations induced by deformation energies, and we derive a closed form representation for the Hessian (at the rest state of the energy) for a general class of deformation energies. Based on these spectra and eigenmodes, we derive two shape signatures. One that measures the similarity of points on a surface, and another that can be used to identify features of surfaces.
[preprint pdf, 2.9 MB] [supplementary video, 6.4 MB] [DOI] [BibTex]
Anna Wawrzinek, Klaus Hildebrandt, Konrad Polthier
Koiter's Thin Shells on Catmull-Clark Limit Surfaces
In: Proceedings of the 16th International Workshop on Vision, Modeling, and Visualization 2011.
We present a discretization of Koiter's model of elastic thin shells based on a finite element that employs limit surfaces of Catmull–Clark's subdivision scheme. The discretization can directly be applied to control grids of Catmull–Clark subdivision surfaces, and, therefore, integrates modeling of Catmull–Clark subdivision surfaces with analysis and optimization of elastic thin shells. To test the discretization, we apply it to standard examples for physical simulation of thin shells and compute free vibration modes of thin shells. Furthermore, we use the discrete shell model to set up a deformation-based modeling system for Catmull–Clark subdivision surfaces. This system integrates modeling of subdivision surfaces with deformation-based modeling and allows to switch back and forth between the two different approaches to modeling.
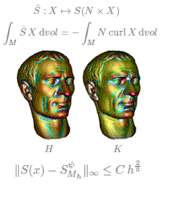
Klaus Hildebrandt, Konrad Polthier
Generalized Shape Operators on Polyhedral Surfaces
In: Computer Aided Geometric Design, Volume 28, Issue 5, June 2011, p. 321-343.
This work concerns the approximation of the shape operator of smooth surfaces in R3 from polyhedral surfaces. We introduce two generalized shape operators that are vector-valued linear functionals on a Sobolev space of vector fields and can be rigorously defined on smooth and on polyhedral surfaces. We consider polyhedral surfaces that approximate smooth surfaces and prove two types of approximation estimates: one concerning the approximation of the generalized shape operators in the operator norm and one concerning the pointwise approximation of the (classic) shape operator, including mean and Gaussian curvature, principal curvatures, and principal curvature directions. The estimates are confirmed by numerical experiments.
[preprint pdf, 1.2 MB] [DOI] [BibTex]
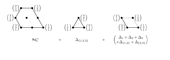
Minkowski decompositions of associahedra presented at 23rd FPSAC 2011, Reykjavik (611-622 of proceedings).
Realisations of associahedra can be obtained from the classical permutahedron by removing some of its facets and the set of facets is determined by the diagonals of certain labeled convex planar $n$-gons as shown by Hohlweg and Lange (2007). Ardila, Benedetti, and Doker (2010) expressed polytopes of this type as Minkowski sums and differences of scaled faces of a standard simplex and computed the corresponding coefficients $y_I$ by M\"obius inversion from the $z_I$ if tight right-hand sides $z_I$ for all inequalities of the permutahedron are assumed. Given an associahedron of Hohlweg and Lange, we first characterise all tight values $z_I$ in terms of non-crossing diagonals of the associated labeled $n$-gon, simplify the formula of Ardila et al., and characterise the remaining terms combinatorially.
[pdf, 0.5 MB] [BibTex]

Combinatorics of Minkowski decompositions of associahedra presented at 23rd CCCG2011, Toronto (pp 611-622 of proceedings).
Realisations of associahedra can be obtained from the classical permutahedron by removing some of its facets and the set of these facets is determined by the diagonals of certain labeled convex planar $n$-gons as shown by Hohlweg and Lange (2007). Ardila, Benedetti, and Doker (2010) expressed polytopes of this type as Minkowski sums and differences of dilated faces of a standard simplex and computed the corresponding coefficients $y_I$ by M\"obius inversion. Given an associahedron of Hohlweg and Lange, we give a new combinatorial interpretation of the values~$y_I$: they are the product of two signed lengths of paths of the labeled $n$-gon. We also discuss an explicit realisation of a cyclohedron to show that that the formula of Ardila, Benedetti, and Doker does not hold for generalised permutahedra not in the deformation cone of the classical permutahderon.
[pdf, 0.5 MB] [BibTex]

Klaus Hildebrandt, Konrad Polthier
On approximation of the Laplace–Beltrami operator and the Willmore energy of surfaces.
In: Computer Graphics Forum, Volume 30, Issue 5, August 2011, Pages 1513-1520. Proceedings of ACM Siggraph/Eurographics Symposium on Geometry Processing 2011.
1st prize best paper award at SGP 2011
Discrete Laplace–Beltrami operators on polyhedral surfaces play an important role for various applications in geometry processing and related areas like physical simulation or computer graphics. While discretizations of the weak Laplace–Beltrami operator are well-studied, less is known about the strong form. We present a principle for constructing strongly consistent discrete Laplace–Beltrami operators based on the cotan weights. The consistency order we obtain, improves previous results reported for the mesh Laplacian.Furthermore, we prove consistency of the discrete Willmore energies corresponding to the discrete Laplace–Beltrami operators.
[pdf, 0.3 MB] [DOI] [BibTex]
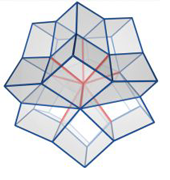
Matthias Nieser, Ulrich Reitebuch, Konrad Polthier
CubeCover - Parameterization of 3D Volumes
In: Computer Graphics Forum, Volume 30, Issue 5, August 2011, Pages 1397-1406. Proceedings of ACM Siggraph/Eurographics Symposium on Geometry Processing 2011.
Despite the success of quad-based 2D surface parameterization methods, effective parameterization algorithms for 3D volumes with cubes, i.e. hexahedral elements, are still missing. CubeCover is a first approach for generating a hexahedral tessellation of a given volume with boundary aligned cubes which are guided by a frame field. The input of CubeCover is a tetrahedral volume mesh. First, a frame field is designed with manual input from the designer. It guides the interior and boundary layout of the parameterization. Then, the parameterization and the hexahedral mesh are computed so as to align with the given frame field. CubeCover has similarities to the QuadCover algorithm and extends it from 2D surfaces to 3D volumes. The paper also provides theoretical results for 3D hexahedral parameterizations and analyses topological properties of the appropriate function space.
[pdf, 3.3 MB] [DOI] [BibTex]
Christoph von Tycowicz, Felix Kälberer, Konrad Polthier
Context-Based Coding of Adaptive Multiresolution Meshes
In: Computer Graphics Forum, Volume 30, Issue 8, pages 2231-2245, December 2011.
Multiresolution meshes provide an efficient and structured representation of geometric objects. To increase the mesh resolution only at vital parts of the object, adaptive refinement is widely used. We propose a lossless compression scheme for these adaptive structures that exploits the parent-child relationships inherent to the mesh hierarchy. We use the rules that correspond to the adaptive refinement scheme and store bits only where some freedom of choice is left, leading to compact codes that are free of redundancy. Moreover, we extend the coder to sequences of meshes with varying refinement. The connectivity compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 7. For efficient compression of vertex positions we adapt popular wavelet-based coding schemes to the adaptive triangular and quadrangular cases to demonstrate the compatibility with our method. Akin to state-of-the-art coders, we use a zerotree to encode the resulting coefficients. Using improved context modeling we enhanced the zerotree compression, cutting the overall geometry data rate by 7% below those of the successful Progressive Geometry Compression. More importantly, by exploiting the existing refinement structure we achieve compression factors that are 4 times greater than those of coders which can handle irregular meshes.
[pdf, 1.4 MB] [DOI] [BibTex]

Matthias Nieser, Jonathan Palacios, Konrad Polthier, Eugene Zhang
Hexagonal Global Parameterization of Arbitrary Surfaces
In: IEEE Transactions on Visualization and Computer Graphics, vol. 18, no. 6, pp. 865-878, June 2012, doi:10.1109/TVCG.2011.118.
In this paper we introduce hexagonal global parameterizations, a new type of parameterization in which parameter lines respect six-fold rotational symmetries (6-RoSy). Such parameterizations enable the tiling of surfaces with regular hexagonal texture and geometry patterns and can be used to generate high-quality triangular remeshing. To construct a hexagonal parameterization given a surface, we provide an automatic technique to generate a 6-RoSy field that respects directional and singularity features in the surface. We also introduce a technique for automatically merging and cancelling singularities. This field will then be used to generate a hexagonal global parameterization by adapting the framework of QuadCover parameterization. We demonstrate the usefulness of our geometry-aware global parameterization with applications such as surface tiling with regular textures and geometry patterns and triangular remeshing.
[preprint pdf, 4.8 MB] [DOI] [BibTex]

Matthias Nieser, Konstantin Poelke, Konrad Polthier
Automatic Generation of Riemann Surface Meshes
In: Advances in Geometric Modeling and Processing, Lecture Notes in Computer Science 6130, Springer Berlin/Heidelberg, pp 161-178, 2010.
Riemann surfaces naturally appear in the analysis of complex functions that are branched over the complex plane. However, they usually possess a complicated topology and are thus hard to understand. We present an algorithm for constructing Riemann surfaces as meshes in R^3 from explicitly given branch points with corresponding branch indices. The constructed surfaces cover the complex plane by the canonical projection onto R^2 and can therefore be considered as multivalued graphs over the plane – hence they provide a comprehensible visualization of the topological structure. Complex functions are elegantly visualized using domain coloring on a subset of C. By applying domain coloring to the automatically constructed Riemann surface models, we generalize this approach to deal with functions which cannot be entirely visualized in the complex plane.
[pdf, 2.6 MB] [DOI] [BibTex]

Klaus Hildebrandt, Christian Schulz, Christoph von Tycowicz, Konrad Polthier
Eigenmodes of surface energies for shape analysis
In: Advances in Geometric Modeling and Processing (Proceedings of Geometric Modeling and Processing 2010), Lecture Notes in Computer Science 6130, Springer, pp 296-314.
In this work, we study the spectra and eigenmodes of the Hessian of various discrete surface energies and discuss applications to shape analysis. In particular, we consider a physical model that describes the vibration modes and frequencies of a surface through the eigenfunctions and eigenvalues of the Hessian of a deformation energy, and we derive a closed form representation for the Hessian (at the rest state of the energy) for a general class of deformation energies. Furthermore, we design a quadratic energy, such that the eigenmodes of the Hessian of this energy are sensitive to the extrinsic curvature of the surface. Based on these spectra and eigenmodes, we derive two shape signatures. One that measures the similarity of points on a surface, and another that can be used to identify features of the surface. In addition, we discuss a spectral quadrangulation scheme for surfaces.
[pdf, 10.6 MB] [DOI] [BibTex]

Ulrich Bauer, Konrad Polthier, Max Wardetzky
Uniform Convergence of Discrete Curvatures from Nets of Curvature Lines
In: Discrete and Computational Geometry Vol. 43, pp: 798-823 (2010).
We study discrete curvatures computed from nets of curvature lines on a given smooth surface and prove their uniform convergence to smooth principal curvatures. We provide explicit error bounds, with constants depending only on properties of the smooth limit surface and the shape regularity of the discrete net.
[pdf, 0.7 MB] [DOI] [BibTex]
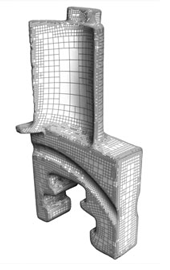
Matthias Nieser, Konrad Polthier, Christian Schulz
Patch Layout from Feature Graph
In: Computer-Aided Design 42(3), pp. 213 - 220, 2010.
Structuring of surface meshes is a labor intensive task in reverse engineering. For example in CAD, scanned triangle meshes must be divided into characteristic/uniform patches to enable conversion into high-level spline surfaces. Typical industrial techniques, like rolling ball blends, are very labor intensive. We provide a novel, robust and quick algorithm for the automatic generation of a patch layout based on a topology consistent feature graph. The graph separates the surface along feature lines into functional and geometric building blocks. Our algorithm then thickens thickens the edges of the feature graph and forms new regions with low varying curvature. Further these new regions - so called llets and node patches - will have highly smooth boundary curves making it an ideal preprocessor for a subsequent spline tting algorithm.
[pdf, 5.6 MB] [DOI][BibTex]
Felix Kälberer, Konrad Polthier, Christoph von Tycowicz
Lossless Compression of Adaptive Multiresolution Meshes
In: Sibgrapi 2009 Technical Paper.
We present a novel coder for lossless compression of adaptive multiresolution meshes that exploits their special hierarchical structure. The heart of our method is a new progressive connectivity coder that can be combined with leading geometry encoding techniques. The compressor uses the parent/child relationships inherent to the hierarchical mesh. We use the rules that accord to the refinement scheme and store bits only where it leaves freedom of choice, leading to compact codes that are free of redundancy. To illustrate our scheme we chose the widespread red-green refinement, but the underlying concepts can be directly transferred to other adaptive refinement schemes as well. The compression ratio of our method exceeds that of state-of-the-art coders by a factor of 2 to 3 on most of our benchmark models.
[pdf, 3.3 MB] [DOI] [BibTex]

Matthias Nieser, Konrad Polthier
Parameterizing Singularities of Positive Integral Index
In: LNCS - Mathematics of Surfaces XIII, Springer 2009, vol. 5654/2009, pp. 265-277.
Classical surface parameterization algorithms often place singularities in order to enhance the quality of the resulting parameter map. Unfortunately, singularities of positive integral index (as the north pole of a sphere) were not handled since they cannot be described with piecewise linear parameter functions on a triangle mesh. Preprocessing is needed to adapt the mesh connectivity. We present an extension to the QuadCover parameterization algorithm, which allows to handle those singularities. A singularity of positive integral index can be resolved using bilinear parameter functions on quadrilateral elements. This generalization of piecewise linear functions for quadrilaterals enriches the space of parameterizations. The resulting parameter map can be visualized by textures using a rendering system which supports quadrilateral elements, or it can be used for remeshing into a pure quad mesh.
[pdf, 2.8 MB] [DOI] [BibTex]

Felix Kälberer, Matthias Nieser, Konrad Polthier
Stripe Parameterization of Tubular Surfaces
In: Topological Data Analysis and Visualization: Theory, Algorithms and Applications, V. Pascucci and H. Hagen and J. Tierny and X. Tricoche (eds.) Springer 2011.
We present a novel algorithm for automatic parameterization of tube-like surfaces of arbitrary genus such as the surfaces of knots, trees, blood vessels, neurons, or any tubular graph with a globally consistent stripe texture. We use the principal curvature frame field of the underlying tube-like surface to guide the creation of a global, topologically consistent stripe parameterization of the surface. Our algorithm extends the QuadCover algorithm and is based, first, on the use of so-called projective vector fields instead of frame fields, and second, on different types of branch points. That does not only simplify the mathematical theory, but also reduces computation time by the decomposition of the underlying stiffness matrices.

Carsten Lange, Konrad Polthier und Udo Simon
Zur Geometrie von Frühstückseiern
In: Mathematische Semesterberichte, (56) 1-14, 2009.
Die euklidische Geometrie von Eiflächen und Eikörpern bietet eine gute Gelegenheit, mathematischen Laien geometrische Begriffsbildungen und Sachverhalte aus der Flächentheorie plausibel zu machen. In dieser Arbeit erörtern wir die erstaunliche Stabilität von Eierschalen und dazu verwandte Probleme unter heuristisch-mathematischen Gesichtspunkten.
[pdf, 294 KB] [DOI] [BibTex]

Konstantin Poelke, Konrad Polthier
Lifted Domain Coloring
In: Computer Graphics Forum, Volume 28, Number 3, June 2009 , pp. 735-742(8).
Complex-valued functions are fundamental objects in complex analysis, algebra, differential geometry and in many other areas such as numerical mathematics and physics. Visualizing complex functions is a non-trivial task since maps between two-dimensional spaces are involved whose graph would be an unhandy submanifold in four-dimensional space. The present paper improves the technique of “domain coloring” in several aspects: First, we lift domain coloring from the complex plane to branched Riemann surfaces, which are essentially the correct domain for most complex functions. Second, we extend domain coloring to the visualization of general 2-valued maps on surfaces. As an application of such general maps we visualize the Gauss map of surfaces as domain colored plots and establish a link to current surface parametrization techniques and texture maps. Third, we adjust the color pattern in domain and in image space to produce higher quality domain colorings. The new color schemes specifically enhance the display of singularities, symmetries and path integrals, and give better qualitative measures of the complex map.
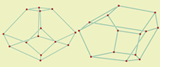
Nantel Bergeron, Christophe Hohlweg, Carsten Lange und Hugh Thomas
Isometry classes of generalised associahedra
In: Séminaire Lotharingien de Combinatoire, 61A (special issue in memoriam Pierre Leroux) (2009), Article B61Aa, 13pp.
Let W be a finite Coxeter group. Generalized associahedra are convex polytopes constructed from a permutahedron of W and an orientation of the Coxeter graph of W. They play a fundamental role in the theory of finite type cluster algebras initiated by Fomin and Zelevinsky, and also appear in algebraic topology. In this article, we show that the isometries of these polytopes are given by certain automorphisms of oriented Coxeter graphs.
[pdf, 0.4 MB] [BibTex]
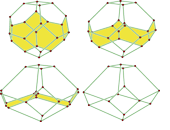
Christophe Hohlweg, Carsten Lange, Hugh Thomas
Permutahedra and generalised associahedra
In: Advances in Mathematics 226 (2011), pp.608-640
Given a finite Coxeter system (W,S) and a Coxeter element c, or equivalently an orientation of the Coxeter graph of W, we construct a simple polytope whose outer normal fan is Nathan Reading's Cambrian fan F(c), settling a conjecture of Reading that this is possible. We call this polytope the c-generalized associahedron. Our approach generalizes Jean-Louis Loday's realization of the associahedron (a type A c-generalized associahedron whose outer normal fan is not the cluster fan but a coarsening of the< Coxeter fan arising from the Tamari lattice) to any finite Coxeter group. A crucial role in the construction is played by the c-singleton cones, the cones in the c- Cambrian fan which consist of a single maximal cone from the Coxeter fan. Moreover, if W is a Weyl group and the vertices of the permutahedron are chosen in a lattice associated to W, then we show that the vertices of our realizations are lattice points.
[pdf, 550 KB] [DOI] [BibTex]

Detection of Planar Regions in Volume Data for Topology Optimization
In: Proceedings of Geometry Modelling and Processing 2008, F. Chen and B. Jüttler (eds.), pp. 119–126, Lecture Notes in Computer Science, vol. 4975, Springer.
We propose a method to identify planar regions in volume data using a specialized version of the discrete Radon transform operating on a structured or unstructured grid. The algorithm uses an efficient discretization scheme for the parameter space to obtain a running time of O(N(T log T)), where T is the number of cells and N is the number of plane normals in the discretized parameter space. We apply our algorithm in an industrial setting and perform experiments with real-world data generated by topology optimization algorithms, where the planar regions represent portions of a mechanical part that can be built using steel plate.
[pdf, 2.1MB] [DOI] [BibTex]
Max Wardetzky, Saurabh Mathur, Felix Kälberer, Eitan Grinspun
Discrete Laplace operators: No free lunch
In: Symposium on Geometry Processing, 2007, pp. 33-37.
Discrete Laplace operators are ubiquitous in applications h6ning geometric modeling to simulation. For robustness and efficiency, many applications require discrete operators that retain key structural properties inherent to the continuous setting. Building on the smooth setting, we present a set of natural properties for discrete Laplace operators for triangular surface meshes. We prove an important theoretical limitation: discrete Laplacians cannot satisfy all natural properties; retroactively, this explains the diversity of existing discrete Laplace operators. Finally, we present a family of operators that includes and extends well-known and widely-used operators.
[pdf, 164 KB] [BibTex]

Miklos Bergou, Saurabh Mathur, Max Wardetzky, Eitan Grinspun
TRACKS: Toward Directable Thin Shells
In: Proceedings of SIGGRAPH, 2007.
We combine the often opposing forces of artistic freedom and mathematical determinism to enrich a given animation or simulation of a surface with physically based detail. We present a process called tracking, which takes as input a rough animation or simulation and enhances it with physically simulated detail. Building on the foundation of constrained Lagrangian mechanics, we propose weak-form constraints for tracking the input motion. This method allows the artist to choose where to add details such as characteristic wrinkles and folds of various thin shell materials and dynamical effects of physical forces. We demonstrate multiple applications ranging from enhancing an artist's animated character to guiding a simulated inanimate object.
[pdf, 1.3 MB] [Video, 53.7MB] [DOI] [BibTex]

Akah Garg, Eitan Grinspun, Max Wardetzky, Denis Zorin
Cubic Shells
In: Symposium on Computer Animation, 2007, pp. 91-98.
Hinge-based bending models are widely used in the physically-based animation of cloth, thin plates and shells. We propose a hinge-based model that is simpler to implement, more efficient to compute, and offers a greater number of effective material parameters than existing models. Our formulation builds on two mathematical observations: (a) the bending energy of curved flexible surfaces can be expressed as a cubic polynomial if the surface does not stretch; (b) a general class of anisotropic materials - those that are orthotropic - is captured by appropriate choice of a single stiffness per hinge. Our contribution impacts a general range of surface animation applications, from isotropic cloth and thin plates to orthotropic fracturing thin shells.
[pdf, 0.6 MB] [BibTex]

Ulrich Bauer and Konrad Polthier
Parametric Reconstruction of Bent Tube Surfaces
In: CyberWorld 2007 Conference Proceedings, Workshop "New Advances in Shape Analysis and Geometric Modeling", IEEE 2007.
We present a method for parametric reconstruction of a piecewise defined pipe surface, consisting of cylinder and torus segments, from an unorganized point set. Our main contributions are reconstruction of the spine curve of a pipe surface from surface samples, and approximation of the spine curve by G1 continuous circular arcs and line segments. Our algorithm accurately outputs the parametric data required for bending machines to create the reconstructed tube.
[pdf, 3.48 MB] [DOI] [BibTex]
Felix Kälberer, Matthias Nieser and Konrad Polthier
QuadCover - Surface Parameterization using Branched Coverings
In: Computer Graphics Forum, Eurographics 2007.
We introduce an algorithm for automatic computation of global parameterizations on arbitrary simplicial 2-manifolds whose parameter lines are guided by a given frame field, for example by principal curvature frames. The parameter lines are globally continuous, and allow a remeshing of the surface into quadrilaterals. The algorithm converts a given frame field into a single vector field on a branched covering of the 2-manifold, and generates an integrable vector field by a Hodge decomposition on the covering space. Except for an optional smoothing and alignment of the initial frame field, the algorithm is fully automatic and generates high quality quadrilateral meshes.
[pdf, 1.84 MB] [DOI] [BibTex]

Klaus Hildebrandt and Konrad Polthier
Constraint-based fairing of surface meshes
In: Proceedings of the Eurographics and ACM Symposium on Geometry Processing 2007.
We propose a constraint-based method for the fairing of surface meshes. The main feature of our approach is that the resulting smoothed surface remains within a prescribed distance to the input mesh. For example, specifying the maximum distance in the order of the measuring precision of a laser scanner allows noise to be removed while preserving the accuracy of the scan. The approach is modeled as an optimization problem where a fairness measure is minimized subject to constraints that control the spatial deviation of the surface. The problem is efficiently solved by an active set Newton method.
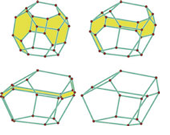
Christophe Hohlweg and Carsten Lange
Realizations of the associahedron and cyclohedron
In: Discrete and Computational Geometry 37: 517-543 (2007).
We describe many different realizations with integer coordinates for the associahedron (i.e. the Stasheff polytope) and for the cyclohedron (i.e. the Bott-Taubes polytope) and compare them to the permutahedron of type A and B respectively. The coordinates are obtained by an algorithm which uses an oriented Coxeter graph of type An or Bn as only input data and which specializes to a procedure presented by J.-L. Loday for a certain orientation of An. The described realizations have cambrian fans of type A and B as normal fan. This settles a conjecture of N. Reading for cambrian lattices of these types.
[pdf, 1.45 MB] [BibTex]

On second-order characteristics of germ-grain models with convex grains
In: Mathematika, 2006, 53 (2), 255-286, ISSN 00255793
For a stationary random closed set Ξ in Rd it is well known that the first-order characteristics volume fraction VV, surface intensity SV and spherical contact distribution function Hs(t) are related by (1- VV)Hs'(0)=SV. In Torquato (2002) an analogous relation between respective second-order characteristics is stated. We give a rigorous proof and sufficient conditions for its validity in case Ξ is a germ-grain model with convex grains. We furthermore obtain formulas for the second-order surface product density if the germ-grain model Ξ is given by a Poisson process or a Gibbs process.
[BibTex]

Max Wardetzky, Miklos Bergou, David Harmon, Denis Zorin, Eitan Grinspun
Discrete Quadratic Curvature Energies
In: Computer Aided Geometric Design (CAGD), 2007, pp. 499-518
We present a family of discrete isometric bending models (IBMs) for triangulated surfaces in 3-space. These models are derived from an axiomatic treatment of discrete Laplace operators, using these operators to obtain linear models for discrete mean curvature from which bending energies are assembled. Under the assumption of isometric surface deformations we show that these energies are quadratic in surface positions. The corresponding linear energy gradients and constant energy Hessians constitute an efficient model for computing bending forces and their derivatives, enabling fast time-integration of cloth dynamics with a two- to three-fold net speedup over existing nonlinear methods, and near-interactive rates for Willmore smoothing of large meshes.
[pdf, 1.21 MB] [Video, 5.9 MB] [Project] [DOI] [BibTex]

Klaus Hildebrandt, Konrad Polthier and Max Wardetzky
On the Convergence of Metric and Geometric Properties of Polyhedral Surfaces
In: Geometriae Dedicata 123 (2006), pp. 89-112.
We provide conditions for convergence of polyhedral surfaces and their discrete geometric properties to smooth surfaces embedded in Euclidian 3-space. The notion of totally normal convergence is shown to be equivalent to the convergence of either one of the following: surface area, intrinsic metric, and Laplace-Beltrami operators. We further show that totally normal convergence implies convergence results for shortest geodesics, mean curvature, and solutions to the Dirichlet problem. This work provides the justification for a discrete theory of differential geometric operators defined on polyhedral surfaces based on a variational formulation.
[pdf, 3.37 MB] [BibTex]
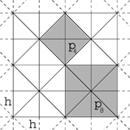
Convergence of the cotan Formula - an Overview
In: Discrete Differential Geometry (A. I. Bobenko, John M. Sullivan, Peter Schröder, Günter Ziegler, eds.), Birkhäuser Basel, 2007.
The cotan formula is a recurrent theme in contemporary discrete differential geometry. In this note we give an overview over its convergence properties on polyhedral surfaces, where convergence is understood in the sense of norms on function spaces. In particular, the notion of mean curvature on a polyhedral surface will serve as a case study; and we will discuss two different concepts of representing it - either as a functional or as a piecewise linear function. We show, how one concept (the functional) converges whereas the other (the function) does in general not.
[pdf, 0.2 MB] [DOI] [BibTex]

The surface pair correlation function for stationary Boolean models
In: Advances in Applied Probability (SGSA) 39(1), 2007, pp. 1-15.
The random surface measure SΞ of a stationary Boolean model Ξ with grains from the convex ring is considered. A sufficient and a necessary condition for the existence of the density of the second-order moment measure of SΞ are given and a representation of this density is derived. As applications, the surface pair correlation functions of a Boolean model with spheres and a Boolean model with randomly oriented right circular cylinders in R3 are determined.
[BibTex]
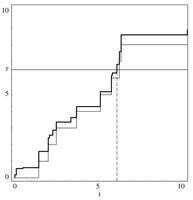
Felix Ballani, Dietrich Stoyan and Susann Wolf
On two damage accumulation models and their size effects
In: Journal of Applied Probability 44(1), 2007, pp. 99-114.
Two cumulative damage models are considered, the inverse gamma process and a composed gamma process. They can be seen as ‘continuous’ analogues of Poisson and compound Poisson processes, respectively. For these models the first passage time distribution functions are derived. Inhomogeneous versions of these process lead to models closely related to the Weibull failure model. All models show interesting size effects.
[BibTex]

Miklos Bergou, Max Wardetzky, David Harmon, Denis Zorin, Eitan Grinspun
A Quadratic Bending Model for Inextensible Surfaces
In: Symposium on Geometry Processing, 2006.
Efficient computation of curvature-based energies is important for practical implementations of geometric modeling and physical simulation applications. Building on a simple geometric observation, we provide a version of a curvature-based energy expressed in terms of the Laplace operator acting on the embedding of the surface. The corresponding energy, being quadratic in positions, gives rise to a constant Hessian in the context of isometric deformations. The resulting isometric bending model is shown to significantly speed up common cloth solvers, and when applied to geometric modeling situations built on Willmore flow to provide runtimes which are close to interactive rates.
[pdf, 0.63 MB] [Project] [BibTex]
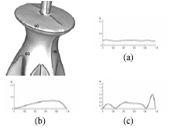
Klaus Hildebrandt, Konrad Polthier and Eike Preuss
Evolution of 3d Curves under Strict Spatial Constraints
In: Ninth International Conference on Computer Aided Design and Computer Graphics (CAD/CG 2005).
We present a new algorithm for fairing of space curves with respect spatial constraints based on a vector valued curvature function. Smoothing with the vector valued curvature function is superior to standard Frenet techniques since the individual scalar components can be modeled similar to curvature-based curve smoothing techniques in 2d. This paper describes a curve smoothing flow that satisfies strict spatial constraints and allows simultaneous control of both curvature functions.
[pdf, 0.2 MB] [DOI] [BibTex]
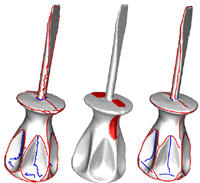
Klaus Hildebrandt, Konrad Polthier and Max Wardetzky
Smooth Feature Lines on Surface Meshes
In: Eurographics Symposium on Geometry Processing (2005).
Feature lines are salient surface characteristics. Their definition involves third and fourth order surface derivatives. This often yields to unpleasantly rough and squiggly feature lines since third order derivatives are highly sensitive against unwanted surface noise. The present work proposes two novel concepts for a more stable algorithm producing visually more pleasing feature lines: First, a new computation scheme based on discrete differential geometry is presented, avoiding costly computations of higher order approximating surfaces. Secondly, this scheme is augmented by a filtering method for higher order surface derivatives to improve both the stability of the extraction of feature lines and the smoothness of their appearance.
[pdf, 1.6 MB] [BibTex]
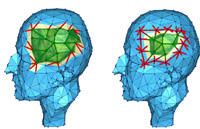
Felix Kälberer, Konrad Polthier, Ulrich Reitebuch and Max Wardetzky
FreeLence - Coding with Free Valences
In: Eurographics 2005.
We introduce FreeLence, a novel and simple single-rate compression coder for triangle manifold meshes. Our method uses free valences and exploits geometric information for connectivity encoding. Furthermore, we introduce a novel linear prediction scheme for geometry compression of 3D meshes. Together, these approaches yield a significant entropy reduction for mesh encoding with an average of 20-30% over leading single-rate region-growing coders, both for connectivity and geometry.
[pdf, 1.72 MB] [BibtTex]

Klaus Hildebrandt and Konrad Polthier
Anisotropic Filtering of Non-Linear Surface Features
In: Eurographics 2004.
A new method for noise removal of arbitrary surface meshes is presented which focuses on the preservation and sharpening of non-linear geometric features such as curved edges and surface regions. Our method uses a non-linear anisotropic geometric diffusion flow for polyhedral surfaces which is based on three new contributions: 1. the definition and efficient calculation of a discrete shape operator and principal curvature properties on polyhedral surfaces that is fully consistent with the known discrete mean curvature representation, 2. an anisotropic discrete mean curvature vector that combines the advantages of the mean curvature normal with the special anisotropic behavior along feature lines of a surface, and 3. an anisotropic prescribed mean curvature flow converging to surfaces with prescribed mean curvature which preserves non-linear features. Additionally our discrete flow is very well suited to prevent boundary shrinkage at constrained and free boundary segments.
[pdf, 2.42 MB] [simulations] [models] [BibTex]

Carsten Lange and Konrad Polthier
Anisotropic Smoothing of Point Sets
In: Special Issue of CAGD 2005.
The use of point sets instead of meshes became more popular during the last years. We present a new method for anisotropic fairing of a point sampled surface using an anisotropic geometric mean curvature flow. The main advantage of our approach is that the evolution removes noise from a point set while it detects and enhances geometric features of the surface such as edges and corners. We derive a shape operator, principal curvature properties of a point set, and an anisotropic Laplacian of the surface. This anisotropic Laplacian reflects curvature properties which can be understood as the point set analogue of Taubin's curvature-tensor for polyhedral surfaces. We combine these discrete tools with techniques from geometric diffusion and image processing. Several applications demonstrate the efficiency and accuracy of our method.
[pdf, 3.52 MB] [simulations] [DOI] [BibTex]

Computational Aspects of Discrete Minimal Surfaces
In: Global Theory of Minimal Surfaces, Proc. of the Clay Mathematics Institute Summer School, J. Hass, D. Hoffman, A. Jaffe, H. Rosenberg, R. Schoen, M. Wolf (Eds.), CMI/AMS, 2005.
In differential geometry the study of smooth submanifolds with distinguished curvature properties has a long history and belongs to the central themes of this field. Modern work on smooth submanifolds, and on surfaces in particular, relies heavily on geometric and analytic machinery which has evolved over hundreds of years. However, non-smooth surfaces are also natural mathematical objects, even though there is less machinery available for studying them. Consider, for example, the pioneering work on polyhedral surfaces by the Russian school around Alexandrov [Aleksandrov/Zalgaller67Intrinsic], or Gromov's approach of doing geometry using only a set with a measure and a measurable distance function [Gromov99Metric]. Also in other fields, for example in computer graphics and scientific computing, we nowadays encounter a strong need for a discrete differential geometry of arbitrary meshes.
[pdf, 1.45 MB] [BibTex]
Mirek Majewski and Konrad Polthier
Using MuPAD and JavaView to Visualize Mathematics on the Internet
In: Proc. of the 9th Asian Technology Conference in Mathematics, (2004), pp. 465-474.
Mathematics education strongly benefits from the interactivity and advanced features of the Internet. The presentation of mathematical concepts on the Internet may go far beyond what we could demonstrate in traditional mathematics textbooks. In this paper we demonstrate, in a number of examples, the additional insight into complex mathematical concepts that can be gained from 3D interactive visualization embedded into web pages. Mathematical visualization is improving our teaching environments and the communication between teachers and students.
[pdf, 0.67 MB] [BibTex]
Polyhedral Surfaces of Constant Mean Curvature
Habilitationsschrift, TU-Berlin (Febr. 2002).
[Chapters1+3+4.pdf, 1.4 MB], [BibTex]
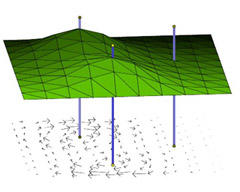
Konrad Polthier and Eike Preuss
Identifying Vector Fields Singularities using a Discrete Hodge Decomposition
In: Visualization and Mathematics III, eds: H.C. Hege, K. Polthier, Springer Verlag, 2003.
[pdf, 2.4 MB] [BibTex]