Research Projects
DFG SFB/Transregio 109 Project C05 - Computational and structural aspects in multi-scale shape interpolation

2020 - 2024
In SFB/Transregio 109 project C05 we investigate shape interpolation, which is a longstanding issue in shape analysis and plays a central role in tasks like shape morphing, the transfer of shape attributes or shape parameterization. Such interpolations entail metrics and correspondences between shapes. Key challenges are landmarks and feature descriptors for correspondence finding and the modeling of deformation fields (choice of coarse-to-fine representation, suitable regularizers and efficient computation).
DAAD PPPI DST/High Fidelity Surface Reconstruction from Noisy Point Sets
2019 - 2021
The process of surface reconstruction aims at the generation of digital geometry models from real world shapes. 3D shape acquisition technologies such as laser scanners or imaging devices produce raw digital data sets (often point sets) of physical shapes which then need to be converted into high-quality geometric representations, e.g. triangle meshes or splines, to best replicate the physical shape. Inevitable problems in surface reconstruction is the presence of noise and outliers due to systemic deficiencies in the data acquisition. Also, surface reconstruction algorithms are often time-consuming due to complexity of the reconstruction algorithm.
In this project, we address key problems in surface reconstruction by developing a feature preserving point set denoising method as a preprocessing step to obtain a cleaned point set without losing feature information for high fidelity surface reconstruction. Furthermore, we are developing a local Delaunay based surface reconstruction algorithm, which takes the preprocessed point set as the input and produces a high-quality triangulated mesh with topological guarantee.
The key objective of this project is to remove spurious noise and outliers and to reconstruct a high-fidelity manifold surface with minimal running time algorithm complexity.
The project is a cooperation between the Geometry Processing group at FU Berlin and Advanced Geometric Computing Lab at IITM in Chennai support by DAAD and DST (Department of Science and Technology).
ECMath/Matheon CH18 - Boundary-Sensitive Hodge Decompositions

2017 - 2018
Based on novel results for smooth and discrete Hodge-type decompositions on manifolds with boundary, this project aims to incorporate discrete boundary-sensitive Hodge decompositions as a central tool for the analysis of blood flow and parameterization of blood vessels. These decompositions provide the following two substantial improvements over existing methods: first, they are able to distinguish harmonic blood flow arising from boundary in- and out flow from harmonic circulations induced by the interior topology of the geometry. Second, they guarantee a theoretically-sound linkage of certain fields with controlled boundary behaviour to cohomological quantities of the geometry, which is the essential and still missing ingredient for the creation of periods to ensure global matching of parameter lines in modern parameterization techniques.
DFG SFB/Transregio 109 Project C05 - Computational and structural aspects of point set surfaces
![]()
2016 - 2020
In project C05 “Computational and structural aspects of point set surfaces”, we develop discrete differential geometric representations for point set surfaces and effective computational algorithms. Instead of first reconstructing a triangle based mesh, our operators act directly on the point set data. The concepts have contact to meshless methods and ansatz spaces of radial basis functions. As proof of concept of our theoretical investigations we transfer and implement key algorithms from surface processing, for example, for surface parametrization and for feature aware mesh filtering on point set surfaces.
DGD SFB/Transregio 109 Project A04 - Integrating discrete geometries and finite element spaces
![]()
2012 - 2016
This project is based on combined efforts in discrete differential geometry and finite element methods for geometric partial differential equations. Especially, discretizations using polyhedral surfaces and piecewise linear functions on them proved to be very successful in both theory and applications. This development led to the creation of counterparts of geometric and metric properties of smooth surfaces on polyhedral surfaces and to insights on convergence properties of them. A geometric ...
Matheon Project F11 - Accelerating Curvature Flows on the GPU

2010
The goal of this project to speed up the computation of curvature flows, previously implemented on the CPU. This project will in particular demonstrate numerics that fully utilize the SIMT (single-instruction, multiple-thread) architecture of modern Graphics cards (GPU), and provide a proof-of-concept implementation of advanced geometry processing on the GPU. In particular, industrial design and CAD companies could use such fast curvature flow or smoothing algorithms for their laser ...
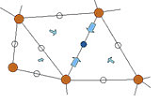
Matheon Project F9 - State Trajectory Compression in Optimal Control
2009 - 2014
For large, nonlinear, and time dependent PDE constrained optimization problems with 3D spatial domain, reduced methods are a viable algorithmic approach. The computation of reduced gradients by adjoint methods requires the storage of 4D data, which can be quite expensive from both a capacity and bandwith point of view. This project investigates lossy compression schemes for storing the state trajectory, based on hierarchical interpolation in adaptively refined meshes as a general predictor.
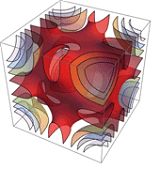
DFG Research Group "Polyhedral Surfaces" - Discrete Implicit Surfaces
2008 - 2012
A discrete implicit surface is considered as the zero set of a scalar-valued function on an ambient 3-dimensional simplicial complex. In contrast to the discrete geometry of simplicial surfaces, the differential operators of implicit surfaces live on the ambient grid. The purpose of this project is to derive a discrete differential geometric toolbox for implicit surfaces similar to (explicit) discrete surfaces. This includes the development of discrete differential operators for implicit ...
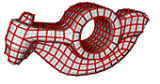
Matheon Project F6 - Multilevel Methods on Manifold Meshes
2004 - 2014
This project addresses the strong needs for multilevel algorithms in industrial applications and in computer graphics where large surface meshes must be efficiently processed. Typical applications are solutions of PDEs on surfaces, surface optimization, and automatic mesh parametrization. Funding is provided by the DFG Research Center MATHEON - "Mathematics for key technologies".
Matheon Project Z3 - Visualization of Algorithms

2004 - 2008
The project develops visualizations and didactic concepts for teaching mathematical algorithms in schools. Understanding how an algorithm works is crucial and often accomplished best by simulating it in some way. Computers provide the means to make these simulations efficient and fun, compared to classical pen-and-paper approaches.
DAAD Project - Multimedia Technology for Mathematics and Computer Science Education

2004 - 2008
This project is a university cooperation between the mathematics institutes of FU Berlin with mathematics institutes at the University of Belgrade, the Mathematics institute of SANU (Serbian Academy of Sciences), the faculties of Sciences and Mathematics, Mechanical Engineering and Electronical Engineering at the University of Nis, the department of Mathematics at the University of Sofia and the department of geometry at the University of Technology and Economics in Budapest, the faculty of ...
Matheon Project F4 - Geometric Shape Optimization
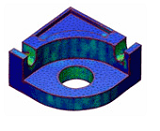
2002 - 2014
Geometric shape optimization is concerned with novel discrete surface energies and computational geometry algorithms for processing and optimizing polyhedral meshes in industrial applications such as computer aided design (CAD) and computer graphics. The main focus of this project addresses the development of efficient mesh processing algorithms and robust modeling tools. The mathematical tools are novel discrete differential and curvature operators.
Matheon Project F1 - Discrete Differential Geometry
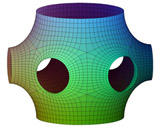
2002 - 2006
This is another project within the DFG Research Center MATHEON - "Mathematics for key technologies". The main goal of this project is the discretization of classical differential geometry: to find proper discrete analogs of differential geometric objects, notions, and methods, and to develop a corresponding theory. Such a discrete differential geometry has applications in computer graphics, numerics, and visualization.
DAAD Project - Development of Electronic Information Infrastructure and Multimedia Courseware
2002 - 2003
This project splits into two parts: Mathematical Visualization and web based software on the hand, and Electronic Information and Communication on the other. The goal is the development of multimedia courseware and the establishment of a cooperative networks for enhanced knowledge transfer. "Development of Electronic Information Infrastructure and Multimedia Courseware" is a project within the DAAD-Sonderprogramm "Akademischer Neuaufbau Südosteuropa".
