The project addresses the strong needs for multilevel algorithms in industrial applications and in computer graphics where large surface meshes must be efficiently processed. Typical applications are solutions of PDEs on surfaces, surface optimization, and automatic mesh parametrization. Such applications are also studied in F4, F2, F1 which will be natural cooperation partners. The focus in F6 is on multilevel methods and hierarchical mesh representations. The project is an outcome of the Matheon TANDEM Workshop "Nichtlineare Optimierung und Discrete Geometrie" held on July 15 and 16, 2004, where a strong need for multilevel methods was encountered in the existing industrial projects in F4. For example, meshes in current CAD applications of the automobil industry often exceed 1 million unknowns.

Scientific Progress

Quadrilateral Surface Parameterization. We developed the QuadCover algorithm to automatically compute a globally consistent quadrilateral parameterization of an unstructured triangular manifold mesh. The parameter lines align with a user-defined frame field, e.g., the principal curvature directions. Not only is such a quad parameterization an ideal starting point for constructing a nested quad hierarchy, but also allows for other applications: Stripe parameterizations of tubular objects such as human blood vessels or neurons are very useful for the visualization of medical data.

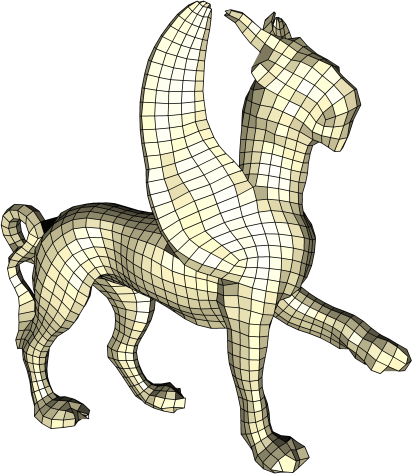
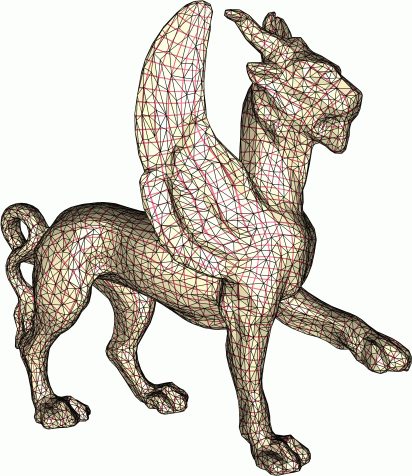
Hexagonal Surface Parameterization. We introduced hexahedral parameterizations, a new type of global parameterizations that tile a surface with patterns of six-fold rotational symmetries. Parameter lines in a hexagonal parameterization intersect at an angle of Pi/3, which enables triangular remeshing of a mesh surface with close to ideal aspect ratios in the triangles.

The parameterization aligns to a six-fold symmetric guidance frame-field. Like in the quadrilateral case, we would like to align the parameter lines with the principal curvature directions. However, there are three parameter lines and two principal directions at each point. Consequently, it is impossible to make use of both principal directions without incurring angular distortion. We note that this challenge is unique to six-fold symmetric fields. We have introduced a method for generating a frame--field with sixfold symmetries which aligns to one of the two principal curvature directions in each point. We also provided a clustering method for singularities for generating smoother fields which leads to more regular parameterizations. This clustering method can also be applied to the quadrangular case.

Hexahedral Volume Parameterization. We invented novel techniques for generating a regular hexahedral mesh of a 3D volume bounded by a given triangular surface. Among the optimization goals are alignment of the voxels with the bounding surface as well as simplicity of the voxel grid. Since volume parameterization is conceptually harder than the surface case it is not straight forward to extend existent 2D methods to 3D. We formulated the theoretical foundations for volume parameterizations including an understanding of the nature of singularities in the volume.

Riemann Surfaces. From a theoretical viewpoint, the topology of the solution space for parameterizations is equivalent to a branched covering surface with 4 (QuadCover), 6 (HexCover) or 24 (CubeCover) many sheets. This insight is fundamental and provides a nice connection between parameterizations and Riemann Surfaces. In this context, we invented a visualization technique for Riemann surfaces and proposed an application to domain coloring.

Multilevel Methods. We extended the nonsmooth Schur-Newton approach to nonsmooth convex minimization problems with PDE constraints and related nonsmooth saddle point problems with anisotropic leading order terms.

The algorithm uses nonsmooth Newton techniques for the Schur complement within a descent method. Suitable damping leads to a globally convergent method that exhibits fast local convergence. Numerical experiments show mesh independent convergence for nested iteration. Moreover the method is robust with respect to degenerating nonsmooth nonlinearities and with respect to (sufficiently smooth) anisotropy.

A feature of nonsmooth Schur-Newton methods is to approximate the given nonsmooth nonlinear problem by a suitable sequence of linear problems. Thus these methods can directly be applied for PDEs on surfaces using linear multilevel solvers developed in an earlier project stage.