We study discrete differential operators on triangulated surfaces and point sets, and develop stable algorithms for industrial problems in geometry processing.

Applications:

• Interactive deformation-based surface modeling.
• Koiter's thin shells on Catmull Clark's subdivision limit surfaces.
• Shape signatures.
• Constraint-based fairing.
• Domain coloring.
• Geometric feature recognition.
• Reconstruction of tubular surfaces.
• Anisotropic geometric diffusion of meshes.
• Feature line extraction for mesh segmentation.
• Digital geometry compression.
• Vector field analysis and discrete Hodge theory.
• Web-based software and visualization algorithms.

Deformation-based modeling of a dragon model. Handles (blue areas) can be moved and rotated in space to the define a deformation.

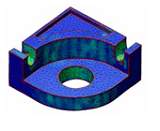
Interactive deformation-based surface modeling. We have developed a framework for deformation-based modeling of surfaces that is interactive, robust, and intuitive to use. A major advantage of deformation-based modeling over traditional modeling techniques like NURBS or subdivision surfaces is that typical modeling operations can be described by few constraints. This allows for efficient and simple click-and-drag user interfaces. The deformations are described by a non-linear optimization problem whose solutions are static states of elastic shells under external forces which implement the user input. A video demonstrating our method is available here.

Testing our discretization against an analytic solution.

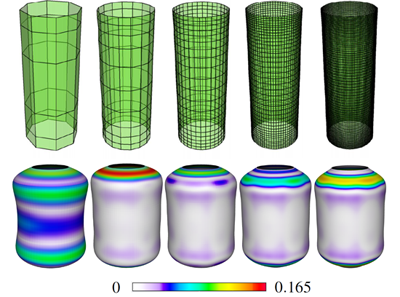Koiter's thin shell on Catmull-Clark's subdivision limit surfaces. We have developed a discretization of Koiter's model of elastic thin shells based on a finite element that employs limit surfaces of Catmull-Clark's subdivision scheme. Koiter's thin shells are an example of a model of elastic thin shells that is based on the Kirchhoff-Love assumptions. In this model, a homogenous thin shell of constant thickness is parametrized over a middle surface. The approach is geometric since the potential energy of the shell's inner forces is described by means of the metric tensor and the shape operator of the surface. Static states of the thin shells are solutions of a 4^th order PDE. Conforming finite element discretizations of this model of thin shells require H²-regular finite elements. Catmull-Clark's subdivision scheme describes a C¹-surfaces as a limit of a refinement process of a coarse intitial grid. Reif and Schröder (2001) proved, that the limit surfaces of Catmull-Clark's subdivision scheme are H²-regular. Furthermore, Stam (1998) developed an efficient scheme for evaluating the limit surface and its derivatives. In combination, these properties allow for any elegant construction of a conforming H² finite element based on Catmull-Clark's subdivision surfaces.

A similarity measure based on our signature is shown. The similarty to the pink dot is measured and color-coded.

Shape signatures. We have studied spectra and eigenfunctions of discrete differential operators that can serve as an alternative to discrete Laplacians for applications in shape analysis. We construct such operators as the Hessians of surface energies, which operate on a discrete function space on the surface, or of deformation energies, which operate on a shape space of surface meshes. In particular, we have designed a quadratic energy such that, on the one hand, its Hessian equals the Laplace operator if the surface is a part of the Euclidean plane, and, on the other hand, the Hessian eigenfunctions are sensitive to the extrinsic curvature (e.g. sharp bends) on curved surfaces. Furthermore, we have considered eigenvibrations induced by deformation energies, and we have derived a closed form representation for the Hessian (at the rest state of the energy) for a general class of such deformation energies. Based on these spectra and eigenmodes, we derive two shape signatures. One that can be used to measures the similarity of points on a surface, and another that can be used to identify features of surfaces.

Results of our constraint-based fairing method.

Constraint-based fairing. We have developed a constraint-based method for the fairing of surface meshes. The main feature of our approach is that the resulting smoothed surface remains within a prescribed distance to the input mesh. This approach is well suited for noise removal from scan data. Though scan data is measured with high accuracy, it still contains noise. Specifying the maximum distance tolerance in the order of the measuring precision of a laser scanner, our method allows to remove noise from the data while preserving the measuring accuracy. The approach is modeled as an optimization problem where a fairness measure is minimized subject to constraints that control the spatial deviation of the surface. The problem is efficiently solved by an active set Newton method.

Our domain coloring method applied to visualize complex functions.

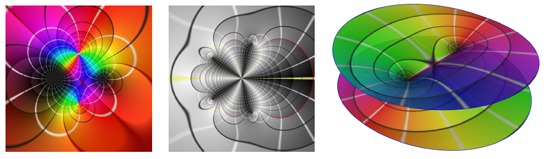Domain coloring. We have developed a domain coloring method for the visualization of complex-valued functions. Our method lifts domain coloring from the complex plane to branched Riemann surfaces, which is the correct domain for many complex functions. New coloring schemes enhance the display of singularities, symmetries and path integrals, and provide new qualitative measures of complex maps.

A volume rendered density function and two planar regions extracted from volume data.

Geometric feature recognition. We have developed and implemented an algorithm to detect planar features in volumetric data. For this algorithm the well-known Hough transform, a standard algorithm for line detection in image processing, has been extended to three-dimensional, unstructured data. Using appropriate data sorting and traversal methods, we achieve a running time of O(mnlog n), where n denotes the input size and m denotes the size of the parameter space discretization.

Results of our parametric reconstruction of tube surfaces.

Reconstruction of tubular surfaces. We have developed a method for reconstructing parametric models of bent tube surfaces from point cloud data. The surface of a bent tube is a piecewise defined pipe surface, consisting of cylinder and torus segments. Our main contributions are reconstruction of the spine curve of a pipe surface from surface samples, and approximation of the spine curve by G1 continuous circular arcs and line segments. Our algorithm accurately outputs the parametric data required for bending machines to create the reconstructed tube.

Results of our anisotropic smoothing method.

Anisotropic smoothing of triangle meshes and point sets. We implement new algorithms for anisotropic fairing of point sampled surfaces as well as triangulated meshes using an anisotropic geometric mean curvature flow. The main advantage of our approach is that the evolution removes noise while it detects and enhances geometric features of the surface such as edges and corners. Currently, this approach is the best method for fairing CAD constructional elements.

From left to right: Original --- Noise added --- Our PMC flow, Eurographics'04.

Extraction of smooth feature lines. Feature lines are salient surface characteristics and guiding lines during surface reconstruction. We have developed a new algorithm for the automatic extraction of smooth feature lines on surface meshes. Our method is based on discrete differential operators and a filtering technique for higher order surface derivatives.

Results of our feature line extraction algorithm, SGP'05.

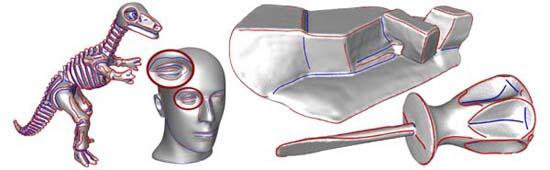Digital geometry compression. Numerical simulations as well as rendering of complex virtual scenes is often limited by the sheer size of the involved geometry meshes. We research the geometric and topological properties of mesh representations to solve the following challenges:

• Efficient and redundant-free representation of 3D geometry meshes.
• Fast online transfer of 3D data sets.
• Creating a toolbox for rapid compression and decompression.

Comparison of denser symbol dispersion of our FreeLence algorithm (left) with symbol dispersion of the popular TG coder, Eurographics'05.

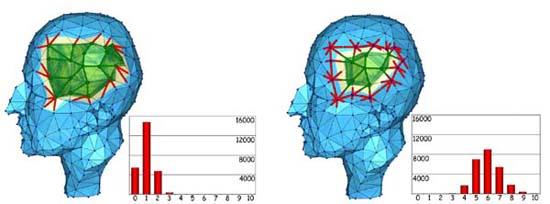Web based software. We set up several new mathematical online services for interactive experiments with 3D geometry, algorithmic treatment of polytopes, archiving a broad range of geometric models as well as online publications of interactive mathematical papers. We interface with computer-algebra systems like Mathematica and Maple - have a look ...

JavaView	EG-models