What is … a van Kampen obstruction cocycle?

This page hosts information on Isaac Mabillard's talk "What is … a van Kampen obstruction cocycle?" at the "What is …?" seminar. The talk will take place on Friday, January 16, 4:00pm in room MA 313 at TU Berlin.

Abstract

The Kuratowski theorem provides a nice criterion for graph planarity, ie, to decide whether a simplicial 1-complex can be embedded into .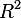

A natural generalization of the problem is to find a criterion to decide whether a simplicial 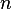-complex 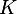can be embedded into 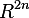. This is what the van Kampen obstruction cocycle gives us. By using standard tricks in PL topology, one can show that 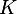is embeddable if and only if (the class of) its cocycle is zero.

This is (maybe?) surprising because embeddability is a geometric question, whereas a cocycle is an algebraic object, but it still carries enough information to solve the geometric problem.

Comments