Was ist eigentlich... ein Ultrafilter?
Diese Seite enthält weitere Informationen, Anregungen und Kritik zum Vortrag "Was ist eigentlich... ein Ultrafilter (und was kann man damit anfangen)?" aus der Reihe Was ist eigentlich...?.Materialien
- Die LaTeX-Beamer Folien, die zur Übersicht dienten, sind in der Attachment-Liste abrufbar.
- Das Video mit integrierten Slides findet man auf http://www.scivee.tv/node/8390 .
Antworten auf Fragen
- Nathan fragte beim Thema Ultrapotenz von
 , ob es auch umgekehrt zu jedem maximalen Ideal des Rings
, ob es auch umgekehrt zu jedem maximalen Ideal des Rings  einen Ultrafilter gibt, so dass die Ultrapotenz gerade dem Quotientenkörper entspricht. Dies ist der Fall
einen Ultrafilter gibt, so dass die Ultrapotenz gerade dem Quotientenkörper entspricht. Dies ist der Fall - Beweis: Sei
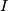 maximales Ideal des Rings. Definiere
maximales Ideal des Rings. Definiere  . Dann ist
. Dann ist 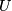 schon Ultrafilter!
schon Ultrafilter! -
 , denn die Nullfolge ist in
, denn die Nullfolge ist in 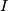 (da additive Unterhalbgruppe);
(da additive Unterhalbgruppe); 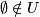 , denn jede Folge, die nirgends
, denn jede Folge, die nirgends 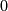 ist, ist invertierbar (durch die Folge der Kehrwerte) --
ist, ist invertierbar (durch die Folge der Kehrwerte) -- 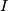 ist aber echtes Ideal, enthält also keine Einheiten.
ist aber echtes Ideal, enthält also keine Einheiten.
- Sind
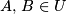 , z.B.
, z.B. 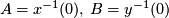 . Dann ist
. Dann ist  (da additive Gruppe) und gerade (!)
(da additive Gruppe) und gerade (!) 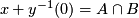 .
.
- Ist
 und
und 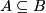 und wieder
und wieder 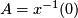 , so ist für die charakteristische Funktion
, so ist für die charakteristische Funktion 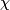 von
von  (die genaue bei den Elementen von
(die genaue bei den Elementen von 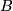 nur
nur 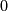 und sonst
und sonst 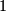 ist) gerade
ist) gerade 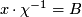 (!!) und
(!!) und 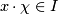 (da Ideal).
(da Ideal).
- Zuletzt sei
 mit
mit 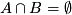 . Dann ist für die jeweiligen charakteristischen Funktionen
. Dann ist für die jeweiligen charakteristischen Funktionen 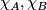 ja gerade
ja gerade 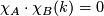 für jedes
für jedes  . Da in einem kommutativen Ring mit Eins jedes maximale Ideal prim ist, folgt, dass schon
. Da in einem kommutativen Ring mit Eins jedes maximale Ideal prim ist, folgt, dass schon 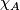 bzw.
bzw. 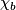 in
in 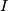 , also
, also 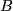 bzw.
bzw. 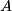 in
in 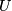 ist. Damit ist der Filter
ist. Damit ist der Filter 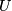 prim, also ein Ultrafilter.
prim, also ein Ultrafilter.
-
- Beweis: Sei
Kleiner Hinweis: Das Argumentieren mit der charakteristischen Funktion ist etwas frickelig, weil die charakteristische Funktion einer Menge gerade dann im Ideal ist, wenn ihr Komplement im Filter ist. Das legt die Formulierung eines Ideal Begriffs dual zum Filterbegriff nahe, wie er auch in der Literatur vorhanden ist, d.h. ein Ideal dual zum Filter besteht aus den Komplementen der Filtermengen, ist abgeschlossen unter Vereinigungen und Teilmengen etc..
Anregungen und Kritik
Hier sollen die Anregungen aus den Kommentaren am Seitenende gesammelt und organisiert werden.
Kommentare
Der Vortrag war "zu kurz" -- Tobias Einwände wurden von mir (Peter) nicht verstanden. Ich hätte ja länger reden können, weil schon viele Fragen während des Vortrags kamen. Vorschlag: "Zeitplanung" sollte nicht vom Vortragenden übernommen werden.
-- krautzbe@PCPOOL/MI/FU-BERLIN.DE - 23 May 2008Latex rendering error!! dvi file was not created.
- User Reference
- BeginnersStartHere
- EditingShorthand
- Macros
- MacrosQuickReference
- FormattedSearch
- QuerySearch
- DocumentGraphics
- SkinBrowser
- InstalledPlugins
- Admin Maintenance
- Reference Manual
- AdminToolsCategory
- InterWikis
- ManagingWebs
- SiteTools
- DefaultPreferences
- WebPreferences
- Categories
 Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Copyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors. Ideas, requests, problems regarding Foswiki? Send feedback


