JVEssentialClasses

This page gives an overview over some essential JavaView packages and classes that are fundamental in most applications.

jv.vecmath

The vecmath package provides classes and methods for linear algebra and simple vector calculations. Important classes are

jv.vecmath.PdVector   // Class for an array of double values.
jv.vecmath.PiVector   // Class for an array of integer values .
jv.vecmath.PdMatrix   // Class for a small (m,n)-matrix of double values
jv.number.PdColor     // Class for a color with red, green and blue components

jv.vecmath.PdVector

A point or a vector in 3D respectively nD space can be represented with an instance of PdVector. A vector also provides several methods for linear algebra calculations.

class PdVector {
  double [] m_data;    // array of double values

  // constructs a vector with given size
  PdVector(int dim) {
    m_data = new double[dim];
  }
  // constructs a vector with two entries
  PdVector(double x, double y) {
    m_data = new double[] {x, y};
  }
  // retrieve a single array component at given index
  double getEntry(int ind) {
    return m_data[ind];
  }
}

Sample usage:

PdVector v   = new PdVector(1., 0.);
PdVector w   = new PdVector(0., 1.);
v.add(w);
double norm  = v.length();

PdVector v   = new PdVector(1., 0.);
PdVector w   = new PdVector(0., 1.);
v.add(w);
double norm  = v.length();

This type also serves as a list for doubles. It can have several flags set. For instance if p is a PdVector which is a point of geom, then p.hasTag(IS_SELECTED) is true iff p is currently selected/marked on the display. In addition it comes with many methods for common vector calculations such as dot and cross product, length, distance, orthogonal projections and so on. Also check the static methods!

jv.vecmath.PiVector

Similar to PdVector, but for integers. May be used as a list/stack for integer values. Use instead of List. New entries can be added to list by calling aPiVector.addEntry(n). This will append the number $n$ to the list. Don't confuse with aPiVector.add(x) which adds the value x to each entry of the vector. An interesting method is removeSuccessiveDuplicates() which does what its name says.

jv.geom

The geom package provides classes and methods for widely used geometry containers such as sets of points, polygons and faces. Important classes are

jv.geom.PgPointSet    // Class for a set of points in 2D, 3D, or nD space.
jv.geom.PgPolygon     // Class for a single polygon.
jv.geom.PgPolygonSet  // Class for a set of polygons sharing points
jv.geom.PgElementSet  // Class for a surface of planar polygonal faces
jv.geom.PgVectorField // Class for a vector field associated to a base geometry
jv.geom.PgTexture     // Class for a texture image

jv.geom.PgPointSet

A set of points in either 2d, 3d, or any n-dimensional ambient space. All points in a point set must have the same dimension.

class PgPointSet {
  int         m_dim;            // uniform dimension of each point
  PdVector [] m_vertex;         // array of all points
  PdVector [] m_vertexNormal;   // optional, a normal vector at each point
  PdColor  [] m_vertexColor;    // optional, a color of each point
  PdVector [] m_vertexTexture;  // optional, a texture position of each point

  // constructor specifies dimension of ambient space
  PgPointSet(int dim) {
    m_dim    = dim;
  }
  // allocate a set of vertices (and, if exist, vertex normals and colors)
  void setNumVertices(int num) {
    m_vertex = new PdVector[num];
    for (int i=0; i<num; i++)
      m_vertex[i] = new PdVector(m_dim);
  }
}

Sample usage:

PgPointSet ps = new PgPointSet(2);
ps.setNumVertices(3);
ps.setVertex(0, 1., 0.);
ps.setVertex(1, 2., 1.);
ps.setVertex(2, 0., 3.);

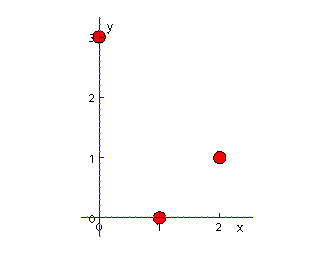
jv.geom.PgElementSet

Polyhedral surface in n-dimensional space is based on a point set.

class PgElementSet extends PgPointSet {
  PiVector [] m_element;        // array of faces
  PdVector [] m_elementNormal;  // optional, a normal of each face
  PdColor  [] m_elementColor;   // optional, a color of each face
  PdVector [] m_elementTexture; // optional, a texture position of each point

  // constructor specifies dimension of ambient space
  PgElementSet(int dim) {
    super(dim);
  }
  // allocate a set of facees (and, if exist, element normals and colors)
  void setNumElements(int num) {
    m_element = new PiVector[num];
    // note: size of individual of elements not known yet
  }
}

Sample usage:

PgElementSet es = new PgElementSet(2);
// Use points of previous point set
es.copy(ps);
es.setNumVertices(4);
es.setVertex(3, 2., 3.);
// Define two triangles
es.setNumElements(2);
es.setElement(0, 0, 1, 2);   // vertex indices of first face
es.setElement(1, 2, 1, 3);   // vertex indices of second face
double area = es.getArea();

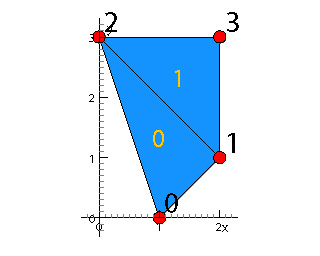Additional useful member methods:

• geom.getVertices(): Returns a list of the vertex indices
• geom.showElementColors(true/false): enables the display of individual element colors in contrast to the global element color which is shown by default. The same story with geom.showVertexColors(true/false).
• geom.showVertices(true/false): Displays the vertices of the geometry.
• geom.setVertexColor/Size/...: Sets individual vertex properties such as color or size. Make sure you have enabled display of individual vertex colors by calling geom.showVertexColors(true) before.
• geom.getElement(i): Returns a PiVector of integers of the vertex indices forming the element with index i.

jv.viewer

Provides functionality for the display and related managing tasks. Important classes:

jv.viewer.PvDisplay    // Class for a single display for viewing.
jv.viewer.PvControl    // Class is a panel to hold several inspectors.
jv.viewer.PvViewer     // Manages several displays and a control panel.
jv.viewer.PgAxes       // Utility class for the coordinate axis and labels.
jv.viewer.PvCamera     // Utility class for a single camera.
jv.viewer.PvLight      // Utility class for a single light.

jv.viewer.PvDisplay

A display is a drawing canvas which shows a collection of geometries:

class PvDisplay extends Canvas {
  // add a geometry to the scene
  void addGeometry(PgGeometryIf geom) { ... }
  // adjust the scene
  void showAxes(boolean flag) { ... }
  void setCamera(int type) { ... }

Sample usage:

PvDisplay disp = new PvDisplay();
disp.addGeometry(es);
disp.setBackground(Color.red);
// insert display to applet (java.awt.Applet or java.awt.Frame)
applet.add(disp);

You can get the currently selected (i.e. active) geometry by

PgElementSet activeGeom = (PgElementSet) m_display.getSelectedGeometry();

jv.number

Utility classes for inspectable numbers and colors. A double or integer may have a slider, and a color may have an color inspector.

Important classes:

jv.number.PuDouble     // Class for a single double with slider.
jv.number.PuInteger    // Class for a single integer with slider.
jv.number.PdColor      // Class for a color with red, green and blue components

These classes provide wrapper for the corresponding native types int, double and so on. They can register action listeners to react on events and ship with a default inspector panel which can be obtained and added to the project info panel using the getInfoPanel() member method. Make sure that this is done in the info panel class' setParent() method, since you need to access the project class instance most likely.

jv.number.PdColor

This class is the JavaView implementation representing a color. Apart from the methods already provided by java.awt.Color it has many additional functions e.g. for conversion, creation and blending between different color formats, both as member methods and static functions.

jv.anim

Animation dialog and containers classes for keyframe animation. Important classes:

jv.anim.PsAnimation    // Class with a play control triggers animated geometries.
jv.anim.PsKeyframe     // Container class for a keyframe animation.

jv.loader

Import and export classes for reading and writing of geometry files. More loader are provided in extension packages jvx.loader and elsewhere. Important classes:

jv.loader.PgLoader     // Optional loader manager determines the correct loader.
jv.loader.PgJvxLoader  // Class for reading/writing a JavaView JVX file.
jv.loader.PgObjLoader  // Class for reading/writing a Wavefront OBJ file.
jv.loader.PgMathLoader // Class for reading/writing a Mathematica file.

Functional Geometric Shapes

jvx.surface

jvx.surface.PgDomain            // Class is rectangle in the (x,y) plane.
jvx.surface.PgGraph             // Graph surface of one scalar function on a planar rectangle.
jvx.surface.PgParmSurface       // Surface of three scalar functions (u(x,y),v(x,y),w(x,y)).
jvx.surface.PgSurfaceOfRotation // Parametrized surface of rotation

jvx.geom

jvx.geom.PgBezierCurve          // Polygon determined by control points
jvx.geom.PgTube                 // Tube surface around a associated polygon
jvx.geom.PgPolygonOnElementSet  // Polygon which lies on an associated element set

dev.primitive

Contains many more functional geometry classes which support the JVF format. Will be discuss later.

Algorithms and Workshops

The advanced algorithms are kept separately from the geometry classes in so-called workshop classes. Workshops will take a, usually a single, geometry and perform some operations on the geometry. When done the workshop is closed.

Workshops derive from a base class which optionally stores a backup geometry and which simplifies the interaction with a user dialog.

jvx.project.PjWorkshop  // Base class for workshops, handles CANCEL and RESET

jvx.geom

jvx.geom.PwClip     // Clips a surface at a user defined level function
jvx.geom.PwGeodesic // Computes geodesic curves on a surface
jvx.geom.PwLIC      // Visualizes a vector field on a surface using textures
jvx.geom.PwNoise    // Adds random noise to vertices of a surface
jvx.geom.PwExplode  // Explodes a surface into parts
jvx.geom.PwSeeds    // Investigates a vector field using particles
jvx.geom.PwUnfold   // Unfolds a surface to a planar region

Projects

A collection of advanced applications. Each application is given by

jv.project.PjProject  // Base class for projects with support for pick events

The vgp Package

Contains more than 50 elaborated research applications as well as tutorials including

vgp.tutor.PjFractalImage         // Computes Mandelbrot and Julia fractals
vgp.tutor.PjTorusKnot            // Curves winding around a torus
vgp.minimal.weier.PjWeierstrass  // Classic minimal surfaces given by Weierstrass equations
vgp.game.life.PjLife             // Games of life on a surface in 3D.
vgp.discrete.harmonic.PjHarmonic // Discrete harmonic maps

Comments

Contains all essential classes from Chapter 2-5. of manual.pdf as of March 2015.

-- KonstantinPoelke - 30 Apr 2015