Anomalous transport in crowded cells and heterogeneous materials
Tracer particles confined to a heterogeneous material
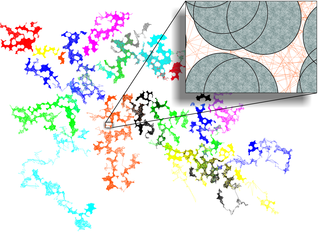
Anomalous transport: particle trajectories in the Lorentz model. Cover page of Phys. Rev. Lett. 96 (16).
Transport of macromolecules and nanoparticles confined by a complex material is typically characterised by a sublinear increase of the mean-square displacement, in contrast to the Brownian motion in a homogeneous solvent. Experiments from many different areas, e.g., protein motion in the cell cytoplasm and in cellular membranes, nanoparticles in polymeric networks, or tracers in porous materials, reveal that anomalous transport is ubiquitous in nature and suggests that slow transport is generic for complex, heterogeneous materials [5].
A paradigm for transport in a spatially heterogeneous medium is provided by the Lorentz model, where tracer particles explore the space between randomly distributed obstacles. The model exhibits a classical localisation transition and displays many facets of anomalous transport like subdiffusion, crossover phenomena, immobilised particles, and persistent dynamic correlations (long-time tails). In a long-standing and fruitful collaboration with Prof. Dr. T. Franosch (University of Innsbruck, Austria) we have established the spatio-temporal transport properties and the dynamic scaling behaviour near criticality including universal scaling functions and corrections to scaling [6,7,8]. Analytic theory served to establish the slow algebraic decay of velocity autocorrelations for Brownian tracers [9].
[5] F. Höfling and T. Franosch, Rep. Prog. Phys. 76, 046602 (2013).
[6] F. Höfling, T. Franosch, and E. Frey, Phys. Rev. Lett. 96, 165901 (2006).
[7] F. Höfling and T. Franosch, Phys. Rev. Lett. 98, 140601 (2007).
[8] A. Kammerer, F. Höfling, and T. Franosch, EPL (Europhys. Lett.) 84, 66002 (2008).
[9] T. Franosch, F. Höfling, T. Bauer, and E. Frey, Chem. Phys. 375, 540 (2010).