Springe direkt zu Inhalt

Design and Analysis of Application Oriented Geometric Algorithms

Projektleitung:
Mitarbeiter/innen:
Förderung:

Deutsche Forschungsgemeinschaft (DFG)

Projektlaufzeit:
01.01.2008 — 31.08.2013
algeng

algeng

In collaboration with

Christian Knauer

 

A project within the DFG Priority Program 1307 Algorithm Engineering.

Summary

The goal of this project is to close a gap between theoretically designed and studied algorithms and the methods that are widely used in practice, especially heuristics. We consider primarily but not exclusively the problem of the geometric shape matching.

There are many algorithms and heuristic methods that work well and are widely used in practice but lack theoretical analysis. We analyze some of such heuristics with respect to the following questions:

  1. What is computed by the method? The quality of the computed results is often not known or even not clearly defined.
  2. What is the running time of the method? In many cases there is a certain trade-off between the running time and the quality of results.

It might be necessary to constraint the inputs of the methods and to characterize the cases that occur in practice in order to be able to perform the analysis.

Besides these theoretical studies we also plan to do prototype implementations of the designed algorithms to verify their practicability. The research focuses on the following problems:

Patterns and shapes

Probabilistic shape matching

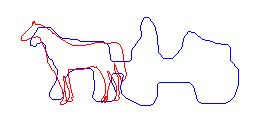
We designed and analyzed a generic probabilistic approach for the shape matching problem. The studied approach is based on an intuitive definition of the shape matching task: Given two shapes A and B find that transformation within the class of allowable transformations which maps B to A in a best possible way. A mapping is considered to be good if large parts of the two shapes coincide within some tolerance distance δ.

The main idea of the probabilistic algorithm is to take random samples of points from both shapes and give a "vote" for that transformation matching one sample with the other. If that experiment is repeated frequently, we obtain by the votes a certain probability distribution in the space of transformations. Maxima of this distribution indicate which transformations give the best match between the two figures. The matching step of the algorithm is, therefore, a voting scheme.

Related methods in the image processing community are the generalized Hough transform, the generalized Radon transform, and the RANSAC algorithm. In contrast to those methods we do not consider a discrete set of features that describe shapes, but work with continuous objects, e.g., curves, regions, and surfaces in 3D. Our method is independent of the choice of the parameterization and the discretization grid in the transformation space.

Our important contribution is the theoretical analysis since it leads to a better understanding of this kind of heuristic techniques. We studied this probabilistic method for several types of shapes in combination with different classes of transformations. We developed and analyzed exactly probabilistic shape matching for two dimensional shapes modeled as sets of line segments and various classes of transformations, such as translations, rigid motions, similarity maps, and affine transformations in general. Prototype implementations experimentally confirmed our results. We showed that the technique can be extended to matching regions instead of curves and to matching higher dimensional volumes.

We started to create a software package for shape matching that has a graphic user interface and can be made publicly available.

 

Figure 1: Partial matching result

input shapes

matching result

transformation space

Symmetry detection

The ongoing Ph.D. thesis of Claudia Dieckmann investigates algorithms for the detection of approximate symmetries in point sets. Here, probabilistic matching can be applied successfully, as implementations show, and also under certain assumptions on the input other efficient algorithms can be found.

Application oriented methods

In the Ph.D. thesis of Fabian Stehn, geometric hybrid registration problems are studied. Registration problems are closely related to geometric matching problems. The term geometric registration problem describes the task of mapping points from one space (pattern space) to their corresponding points in a deformed copy of that space called model space.

This research is motivated by a real world application: navigated surgery. Here, the goal is to register an operation theatre space (pattern space) to the internal coordinate system (model space) of a medical navigation system. The purpose of a medical navigation system is to support surgeons by visualizing the used surgical instruments at their correct position in a 3D-model of a patient. The models are generated beforehand based on CT or MRT scans.

Hybrid registration is a novel strategy to compute solutions for this alignment problem. Geometric hybrid registrations reduce the spatial synchronization problem to a series of (at least two) geometric matching problems that are solved interdependently. Usually, a computationally involved point-to-surface matching is combined with a comparably simpler but underdefined point-to-point matching. The point-to-surface matching is computed for a sufficiently large and suitably distributed set of points (called surface points) measured in the pattern space to a geometric surface in the model space. For the point-to-point matching, a small set of (one to three) characteristic points are measured in the pattern space and are defined in the model space. In the context of the intended application, these points are called anatomic landmarks - anatomically exposed spots within the field of interest.

In the Ph.D. thesis of Sven Scholz the ideas of probabilistic shape matching are applied to a real world question in collaboration with AKTOR KNOWLEDGE TECHNOLOGY NV in Antwerp, Belgium: automatically determining the similarity between trademarks of companies. In particular, after some preprocessing shapes are extracted from the images of trademarks and compared using probabilistic shape matching enhanced with further heuristics. In order to demonstrate the usability of this approach in practice, all these algorithms have been implemented and tested on various sets of figurative images and real-world trademark images. The results of the experiments carried out show a large conformity with human perception of similarity and the operating figures obtained are clearly better than the ones of other existing systems.

Packing and stacking geometric objects

One topic connected with shape matching, which we plan to address, are efficient algorithms for packing and stacking geometric objects. In the plane geometric objects would be, e.g., simple polygons which can be transformed by translations or rigid motions. The objective is to find transformations placing the objects such that some cost function is minimized, for example the area or the perimeter of the convex hull of the union of all transformed figures. The objects may either be overlapping (stacking) or overlapping is not allowed (packing).

Optimal packing of an arbitrary number of objects, even axes-parallel rectangles under translations, can easily shown to be NP-hard. This is an important practical problem in textile or steel industry, namely, cutting out given parts from a large cloth or sheet metal and minimizing the waste. Therefore, numerous heuristic approaches exist from the optimization community. Rigorously analyzed methods with a guaranteed performance have been found so far in the computational geometry community only in special cases.

Realistic input models

Geometric shape matching

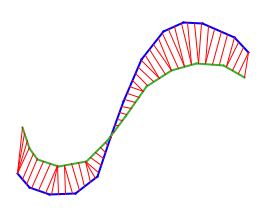
Figure 2: Illustration of the Fréchet distance for polygonal curves

Fréchet distance

For many other distance measure (e.g., the Hausdorff-distance or the area of the symmetric difference) the situation is similar. For the Earth-Mover's-distance (a distance measure for weighted point sets which is very popular in multimedia-retrieval no exact algorithmic solutions are known for the shape matching problem (even for translations in the plane). Again one is forced to turn to approximation methods - unfortunately, even these turn out to be fairly complicated and are not useful for real applications.

The goal is to investigate if and how restrictions to the structure of the input data can be exploited to develop more efficient and conceptually simpler algorithms for this kind of problems.

Geometric search structures

Many search structures for geometric objects are based on the following general (heuristic) approach: For each object a (high-dimensional) feature vector is determined and the similarity of two objects is simply determined by the distance (in some Lp-metric) of the corresponding feature vectors. The vantage-point methods suggest to use the distance (w.r.t. a suitable geometric distance measure δ, like, e.g., the Hausdorff distance) to a small set of fixed so-called vantage-objects from the data set as a feature vector. These methods seem to work very well in practice, but they have not been fully analyzed from a theoretical point of view.

Worst-case time bounds are known only in special cases (like when δ is "close" to the Euclidean metric) and in existing applications the vantage-objects are chosen according to some ad-hoc heuristic.

We aim to analyze this approach in a broader context by first identifying and formalizing the appropriate theoretical questions and concepts, like, e.g., "What is the relation between δ and the Lp-distance of the feature vectors?", "What is a good set of vantage-objects?", or "What is the algorithmic complexity of finding such a good set (approximately)?". In a second step we will try to answer these questions for selected scenarios (geometric objects and distance measures δ) again with the emphasis on appropriate assumptions about realistic input models.

PCA

Principal component analysis (PCA)is one of the oldest and best known techniques of multivariate analysis. Numerous applications of PCA can be found in data compression, visualization, image processing, pattern and image recognition, time series prediction, detecting symmetry, or dimension detection. Most of the applications of PCA are non-geometric in their nature. However, there are also few purely geometric applications like estimation of the undirected normals of the point sets or computing PCA bounding boxes (bounding boxes determined by the principal components of the point set).

We presented closed-form solutions for efficiently updating the principal components of a set of n points, when m points are added or deleted from the point set. For both operations performed on a discrete point set in Rd, we can compute the new principal components in O(m) time for fixed d. This is a significant improvement over the commonly used approach of recomputing the principal components from scratch, which takes O(n + m)time. An important application of the above result is the dynamical computation of bounding boxes based on principal component analysis. We have implemented and evaluated several algorithms for computing dynamically PCA bounding boxes in R3. In addition, we present closed-form solutions for computing dynamically principal components of continuous point sets in R2 and R3. In both cases, discrete and continuous, to compute the new principal components, no additional data structures or storage are needed.

 

Publication list