The fundament of our theoretical studies to characterize a variety of scale-dependent phenomena in the atmosphere is a unified approach [1,2,3,4], which is based on multiple-scales asymptotics. [5], Important results achieved up to now are

Theory:

- Model equations for atmospheric motions on planetary spatial scales [6,7,8], as they are relevant for applications in the climate research, [9],

Change in mean air temperature
at ground level in 2100 for a standard scenario of carbon dioxide emissions.
(Picture provided by
S. Rahmsdorf, PIK Potsdam)

- a theory for the temporal evolution of cyclones, which incorporates the interaction between the internal flow structure, the background flow, and the inclination of the centerline with respect to the vertical. Furthermore, it results in the determination of the effective direction of motion and the vortex speed, [10,11],

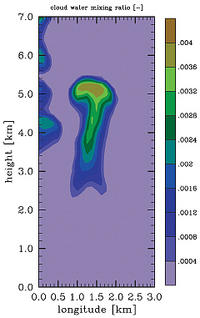
- two mathematical models for the evolution of deep convective clouds and their interaction with the surrounding atmosphere, [12,13,14,15],

Theory and Simulation of Deep Convective Clouds

Clouds play a decisive role in both the dai­ly wea­ther pat­tern and the long-­term cli­mate varia­tion. They con­sti­tute a moi­sture reser­voir carried by the wind and re­pre­sent the pre­limi­nary stage of pre­ci­pita­tion. By reflec­tion, ab­sorp­tion, and trans­mission of electromag-netic waves in the visi­ble and infra­red spectra they in­fluence directly the atmos­phere's heat budget.

For theory development and computer simulation clouds pose a particular chal­lenge since they are deter­mined by the inter­action of a multitude of indivi­dual pro­cesses. Some of them take place in the size range of small cloud drop­lets (micrometres), some in the size range of typical turbu­lent flow fluctua­tions (metres), some in the size range of charac­teristical cumulus clouds (one to ten kilo­metres). Large strato­cumulus cloud layers above the oceans even span several thou­sands of kilo­metres. For this rea­son cloud pro­cesses belong to the class of multi scale phe­no­mena inve­stigated inten­sely by natural scien­tists and mathe­mati­cians these days.

Please click here to see more

- reduced model equations describing the structure and temporal evolution of different types of atmospheric boundary layers. This includes, in one case, the analysis of model uncertainties, [16,17,17a],

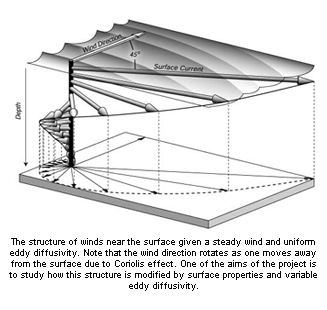
Effects of surface properties on atmospheric boundary layer flows

This project is concerned with a systematic study of effects of the under­lying surface on atmos-­pheric flows and to quan­tify the impact of uncer­tain­ties in sur­face proper­ties on the accu­racy of the boun­dary layer models. The multi­scale asymp­totic method is used to model the boun­dary layer pro­ces­ses captu­ring the spa­tial and tem­poral scales of inte­rests to­gether with the non­linear inter­actions therein. The poly­no­mial chaos method is used in the charac­teri­za­tion of the un­cer­tainty in the flow quan­ti­ties as func­tions of random model inputs such as sur­face rough­ness un­cer­tain­ty.

One of the goals of this in­vesti­gation is to improve on the repre­sen­tation of boun­dary layer pr­ocesses in nume­rical models and also suggest ap­pro­priate coup­ling strate­gies between a boun­dary layer model and the free atmos­phere model. We hope that this will lead to a more accu­rate weather pre­dic­tion and climate fore­casts.

- a critical discussion [18], of well established so called "soundproof" models (where no sound waves are present). This includes different versions of anelastic models [19,20,21,22]and the pseudo-incompressible model[23].

- stochastic models, which efficiently represent certain aspects of weather statistics and planetary fluid mechanics relevant for our climate, [24,25,26,27].

[ 1] Klein, R. (2004) An applied mathematical view of meteorological modeling. Applied Mathematics Entering the 21st century; Invited talks from the ICIAM 2003 Congress., 116 . pp. 177-219.

[ 2] MetStroem lecture notes

[ 3] Klein, R. (2008) An Unified Approach to Meteorological Modelling Based on Multiple-Scales Asymptotics. Advances in Geosciences, 15 . pp. 23-33.

[ 4] Klein, R. (2010) Scale-Dependent Asymptotic Models for Atmospheric Flows. Annual Review of Fluid Mechanics, 42 . (In Press)

[ 5] Schneider, W. (1978) Mathematische Methoden in der Strömungsmechanik, Vieweg

[ 6] Majda, A.J. and Klein, R. (2003) Systematic Multiscale Models for the Tropics. Journal of Atmospheric Sciences, 60 pp. 393-408.

[ 7] Dolaptchiev, S. (2008) Asymptotic models for planetary scale atmospheric motions (phdthesis) Freie Universität Berlin

[ 8] Dolaptchiev, S. and Klein, R. (2009) Planetary geostrophic equations for the atmosphere with evolution of the barotropic flow. Dynamics of Atmospheres and Oceans Volume, 46 (1-4). pp. 46-61

[ 9] Petukhov, V. Et Al (2000)
CLIMBER-2: A climate system model of intermediate complexity. Part I: Model description and performance for the present climate, Journal Climate Dynamics, Volume 16, pp 1-17

[10] Mikusky Dissertation

[11] Mikusky, E. and Owinoh, A.Z. and Klein, R. (2005) On the influence of diabatic effects on the motion of 3D-mesoscale vortices within a baroclinic shear flow. In: Third MIT Conference on Computational Fluid and Solid Mechanics, June 14-17, 2005.

[12] Carqué, G. (2009) Derivation and Validation of an Asymptotic Column Model for Deep Convective Precipitating Clouds. PhD thesis, Freie Universität Berlin.

[13] Carque et al. ZIB/Reports; Carqué, G. and Schmidt, H. and Stevens, B. and Klein, R. (2008) Plausibility Check of an Asymptotic Column Model for Deep Convective Clouds. ZIB-Report, 08 (44)

Carqué, G. and Owinoh, A.Z. and Klein, R. and Majda, A. J. (2008) Asymptotic Scale Analysis of Precipitating Clouds. ZIB-Report , 08-03 . ISSN 1438-0064

[14] Majda, A. J. and Klein, R. (2006) Systematic Multiscale Models for Deep Convection on Mesoscales. Theoretical and Computational Fluid Dynamics, 20

[15] Ruprecht, D. and Klein, R. and Majda, A. J. (2009) Moisture - Gravity Wave Interactions in a Multiscale Environment. Journal of Atmospheric Sciences. Technical Report. Konrad Zuse Zentrum Berlin.

[16] Owinoh, A.Z. and Hunt, J. and Orr, A. and Clark, P. and Klein, R. and Fernando, H. and Nieuwstadt, F. (2005) Effects Of Changing Surface Heat Flux On Atmospheric Boundary-Layer Flow Over Flat Terrain. Boundary Layer Meterology, 116 (2). pp. 331-361.

[17] Klein R., Mikusky E., Owinoh A. (2005) Multiple Scales Asymptotics for Atmospheric Flows,
in: 4th European Conference of Mathematics, Stockholm, Sweden, 2004, Ari Laptev (ed.), 201--220; European Mathematical Society Publishing House,

[17a] Schmidt, H. and Oevermann, M. and Bastiaans, R.J.M. and Kerstein, A.R. (2009) A priori Tabulation of Turbulent Flame Speeds via a Combination of a Stochastic Mixing Model and Flamelet Generated Manifolds, Extended to Incorporate Strain Effects. ZIB Report, 09-09 . ISSN 1438-0064

[18] Klein, R. (2009) Asymptotics, structure, and integration of sound-proof atmospheric flow equations. Theoretical and Computational Fluid Dynamics, 23 (3). pp. 161-195. ISSN 0935-4964 (Print) 1432-2250 (Online)

[22] Bannon, P.R. (1996) On the anelastic approximation for a compressible Atmosphere (article)
Journal J.Atmosph.Sci., 53, pp 3618--3628

[23] Durran, D.R. (1989) Improving the anelastic approximation (article)
Journal of Atmosphere Sciences, 46, pp 1453--1461

[24] Petoukhov, V. and Eliseev, A. and Klein, R. and Oesterle, H. (2008) On the statistics of the free-troposphere synoptic component. Part I: An evaluation of skewnesses and estimation of the third-order moments contribution to the synoptic-scale dynamics and meridional fluxes of heat and humidity. Tellus, 60 (1). pp. 11-31.

[25] Horenko, I. and Dolaptchiev, S. and Eliseev, A. and Mokhov, I. and Klein, R. (2008) Metastable Decomposition of High-Dimensional Meteorological Data with Gaps. Journal of the Atmospheric Sciences, 65 (11). pp. 3479-3496.

[26] Horenko, I. and Klein, R. and Dolaptchiev, S. and Schütte, Ch. (2008) Automated Generation of Reduced Stochastic Weather Models I: Simultaneous Dimension and Model reduction for Time Series Analysis. Mult. Mod. Sim., 6 (4). pp. 1125-1145.

[27] Franzke, Ch. and Horenko, I. and Majda, A. J. and Klein, R. (2009) Systematic Metastable Atmospheric Regime Identification in an AGCM.Journal for Atmospheric Sciences, 66 . pp. 1997-2012.

Complete list of publications