Research
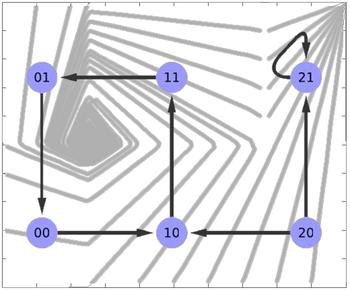
State transition graph with a cyclic attractor emphasized
Image Credit: Hannes Klarner
Discrete versus continuous dynamics
Image Credit: Hannes Klarner
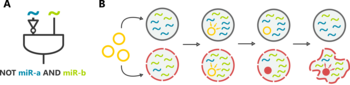
Designing miRNA-based cell classifier circuits using different approaches
Image Credit: Melania Nowicka
In our research we focus on modeling and analyzing biological regulatory networks in cooperation with colleagues from the life sciences, meeting the mathematical challenges posed by such applications. While our main focus lies on discrete approaches, in particular discrete dynamical systems and graph theory, we are interested in mathematical breadth, connecting to continuous and stochastic dynamical systems theory, statistics, formal verification and algebraic geometry.
One focus is to provide modeling and analysis methods respecting the constraints imposed by the available data. Data quality and uncertainties must be carefully taken into account to construct valid models. A major aim of model analysis in turn is to pinpoint ambiguities and generate hypotheses exploitable for experimental design. Combining different theoretical approaches for data analysis and modeling allows to bundle their distinct strengths and to process the available information in a systematic and holistic fashion.
Central to our work are logic-based models, constructed using qualitative observations which are often more abundantly available than the quantitative data needed for building well-supported differential equation models. Analysis of such models can draw on a variety of mathematical methods, e.g., iteration and graph theory as well as methods from formal verification. This allows for comprehensive analysis of complex systems, often uncovering crucial structural and dynamical characteristics. It furthermore makes it possible to analyze multi-cell models as well as to test large numbers of smaller models for consistency with the available data, the latter addressing the parameter identification problem and allowing to evaluate analysis results with respect to data uncertainty.
Our main application here is in the context of oncogenic signaling networks where we investigate, e.g., the influence of crosstalk on drug effects together with colleagues from Charité Berlin, or cell fate determining processes related to metastasis with international partners from molecular biology and the medical sciences. We work on methods for maker detection and network control, immediately related to diagnostics and treatment.
The computational strength of the logical formalism can also be exploited in tandem with more resolved modeling. Combining discrete, continuous and stochastic approaches yields methods tailored to optimally exploit the available data, to evaluate uncertainty and to uncover essential mechanisms of the system as we have done, e.g., for stress response systems in bacteria. An interesting mathematical challenge is to rigorously clarify what properties are preserved between models in different formalisms.
All the methods described above are highly useful for an engineering approach to biological networks as is central for synthetic biology. Here, vast design spaces need to be searched to find optimal models exhibiting a given functionality, taking into account constraints imposed by the limits of what can be actually constructed as a biological circuit in the lab. We exploit the sophisticated machinery available to analyze discrete models to exhaustively test design spaces in two major application. First, we are investigating classifier circuits capable of sensing certain biomarkers and deciding based on the input whether a cell is healthy or diseased.
Second, we are looking for circuits designs for Turing pattern generation in tissues. Both projects are in collaboration with colleagues constructing such circuits in the wet lab.
Evolutionary processes are another interesting area when looking for challenging mathematical problems. With colleagues from paleobiology we started looking into understanding mechanisms of change in biodiversity over hundreds of millions of years. Exploiting fossil records and using temporal networks we track so-called bioregions capturing geographic areas with comparable species composition over time. This calls for developing appropriate temporal clustering methods that can cope with incomplete data. On the other end of the spectrum, we are looking at the molecular level and methods to compute reliable phylogenetic trees. In a recently started cooperation with colleagues from algebraic geometry and bioinformatics we explore a new approach to finding consensus trees using tropical geometry and combinatorial optimization.
As a starting point, we use logic-based models to represent the systems of interest to us. They are based on qualitative observations which are often more abundantly available than the quantitative data needed for constructing well-supported differential equation models. Analysis of such models can draw on a variety of mathematical methods, e.g., iteration and graph theory as well as methods from formal verification. This allows for comprehensive analysis of complex systems, often uncovering crucial structural and dynamical characteristics. It furthermore makes it possible to analyze multi-cell models as well as to test large numbers of smaller models for consistency with the available data, the latter addressing the parameter identification problem and allowing to evaluate analysis results with respect to data uncertainty. Our main application here is in the context of oncogenic signaling networks where we investigate, e.g., the influence of crosstalk on drug effects together with colleagues from Charité Berlin.
The computational strength of the logical formalism can also be exploited in tandem with more resolved modeling. Combining discrete, continuous and stochastic approaches yields methods tailored to optimally exploit the available data, to evaluate uncertainty and to uncover essential mechanisms of the system as we have done, e.g., for stress response systems in bacteria. Such integrated approaches are also promising for data analysis, where statistical methods can be combined with a network-based view to uncover the key players of system functionality. An interesting mathematical challenge is to rigorously clarify what properties are preserved between models in different formalisms.
All the methods described above are highly useful for an engineering approach to biological networks as is central for synthetic biology. Here, vast design spaces need to be searched to find optimal models exhibiting a given functionality, taking into account constraints imposed by the limits of what can be actually constructed as a biological circuit in the lab. We exploit the sophisticated machinery available to analyze discrete models to exhaustively test design spaces in two major application. First, we are investigating classifier circuits capable of sensing certain biomarkers and deciding based on the input whether a cell is healthy or diseased. Second, we are looking for circuits designs for Turing pattern generation in tissues. Both projects are in collaboration with colleagues constructing such circuits in the wet lab.