Shira Faigenbaum - Repairing and Denoising Scattered Data for the Reconstruction of Manifolds Embedded in High Dimensions
Abstract
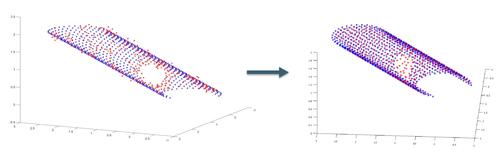
High dimensional data is increasingly available in many fields, and the problem of extracting valuable information from such data is of primal interest. A common assumption is that high dimensional data is an embedding of a low dimensional manifold. Often, the data suffers from presence of noise, outliers, and non-uniform sampling (which may result in 'holes' in the manifold). Standard approximation tools fail to address these problems - even in low dimensions. In our research, we propose to reconstruct the manifold's geometry by extending the Locally Optimal Projection operator (LOP) algorithm [1] to the high dimensional case. Additionally, we utilize our framework to address other challenges rising in high dimensional data: a) calculation of k-multivariate L1-medians; b) smooth manifold repairing; c) up/down data sampling. We will demonstrate the effectiveness of our framework by considering noisy data from manifolds of 2-10 dimensions embedded in R60 (Figure 1). In addition, I will discuss several matters related to surface reconstruction, which will be addressed during my visit to the Freie Universität Berlin.
Biography
Shira Faigenbaum-Golovin is a Ph.D. candidate in applied mathematics at the school of mathematical sciences of Tel Aviv University under the supervision of Prof. D. Levin and Prof. Y. Shkolnisky. Shira´s research interests lie in the area of approximation theory. In her Ph.D. she studies approximation in high dimensional spaces from scattered data. Additionally, Shira is a team member in an interdisciplinary project with the archeological department at TAU. The research focuses on imaging and handwriting comparison of historical documents by developing image processing, pattern recognition, machine learning, and statistics tools. Among her most notable achievements are a paper on algorithmic handwriting analysis published in PNAS and a study revealing a new inscription via multispectral imaging published in PLOS ONE. Project site: shirafaigen.wixsite.com/ostraca.
Time & Location
Sep 13, 2018 | 03:00 PM
FU Berlin | Arnimallee 6 | Raum 108/109