Error aware analysis of multi-scale reactivity models for photo-chemical surface reactions

Project Head: Sebastian Matera

Research Staff: Sandra Döpking

Funding: This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin

Internal cooperation: F. Schmidt (ZIB), Ch. Schütte (FU, ZIB), R. Schneider (TU)

External cooperation: Ch. Scheurer, K. Reuter (TUM), M. J. Hoffmann (Stanford), Aditya (Ashi) Savara (Oak Ridge National Laboratory)

---

Background

On the route to a more efficient exploitation of energy and materials, the design of new heterogenous catalysts is a central aspect, be it for the production of fine chemicals or the conversion of solar energy to fuels. Ideally, such a design is based on an atomistic understanding of the origin of catalytic activity. In order to enable this detailed undestanding, first-principles kinetic Monte Carlo approaches have been established during the last decade. Despite their success, these still have some some limitations. On the one hand, the electronic structure methods, employed to determine required rate parameters, introduce a non-negligible error into the later. On the other hand, the need for stochastic simulation and the typically large dimension of the parameter space hampers the determination of the rate determining steps by sensitivity analysis, i.e. the most interesting input for a rational catalyst design.

The purpose of this project is to address the aforementioned problems by development of tools for local and global sensitivity analyses. These are applied to models from classical catalysis, but also to models for photo-catalytic processes.

Results

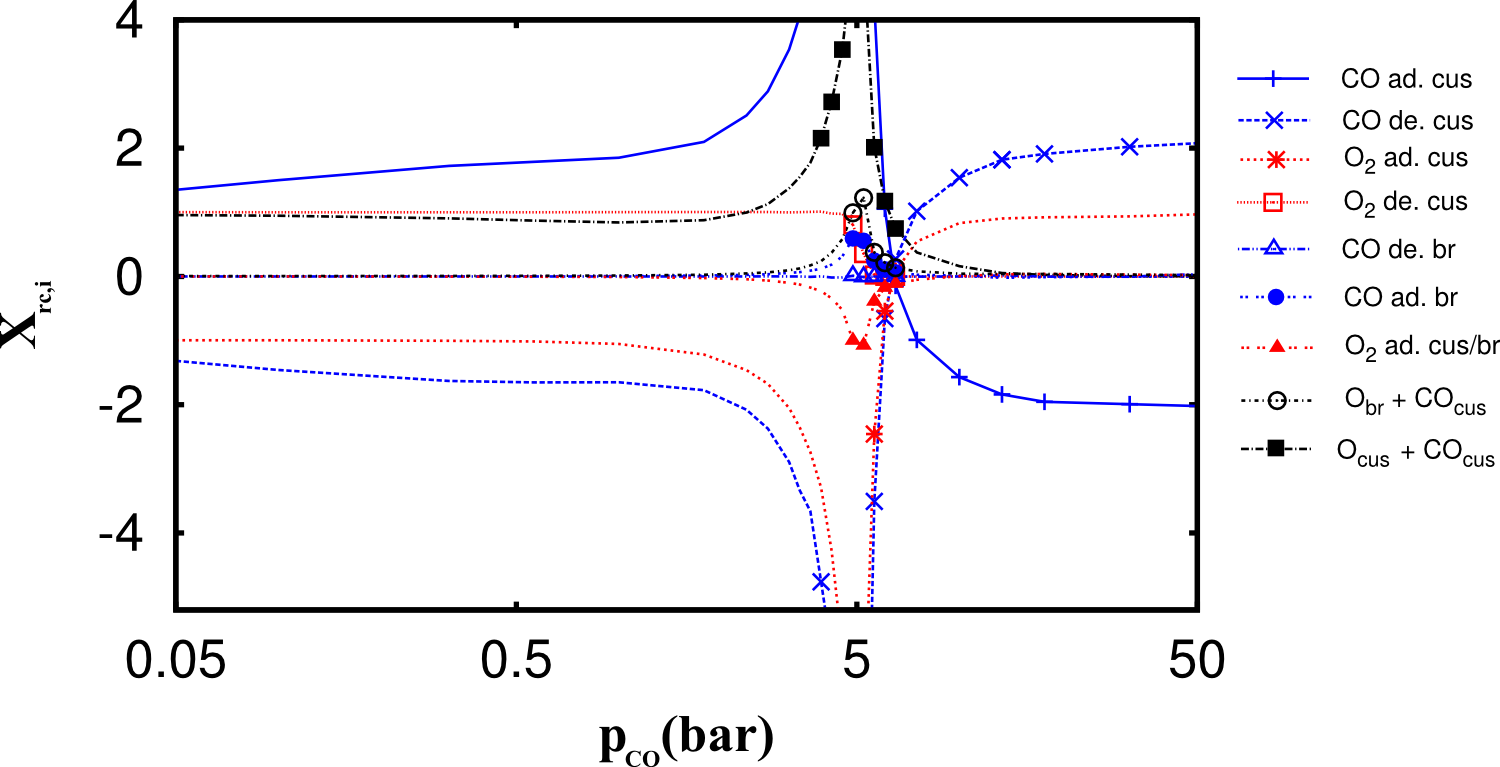
Finite difference approximations for gradient based local sensitivity analysis suffer from the statistical noise in the stochastic simulation results, but also from the typically large number of parameters. In order to accelerate gradient estimation, we have developed a three stage strategy, which significantly reduces the number of necessary finite difference approximations.  In the first stage, bounds for the gradients are sampled from a single trajectory. In the second stage, those gradients with non-vanishing bounds are estimated using a direct sampling approach based on linear response theory. Only those sensitivities, which can not be estimated with sufficient accuracy by one of the previous approaches, are numerically estimated. The above image shows the so-called Degree of Rate Control for the CO oxidation on ruthenium dioxide. The model has 22 parameters, of which only the non-vanishing are shown. Those sensitivities, which needed to be estimated by finite differences, are marked with symbols.

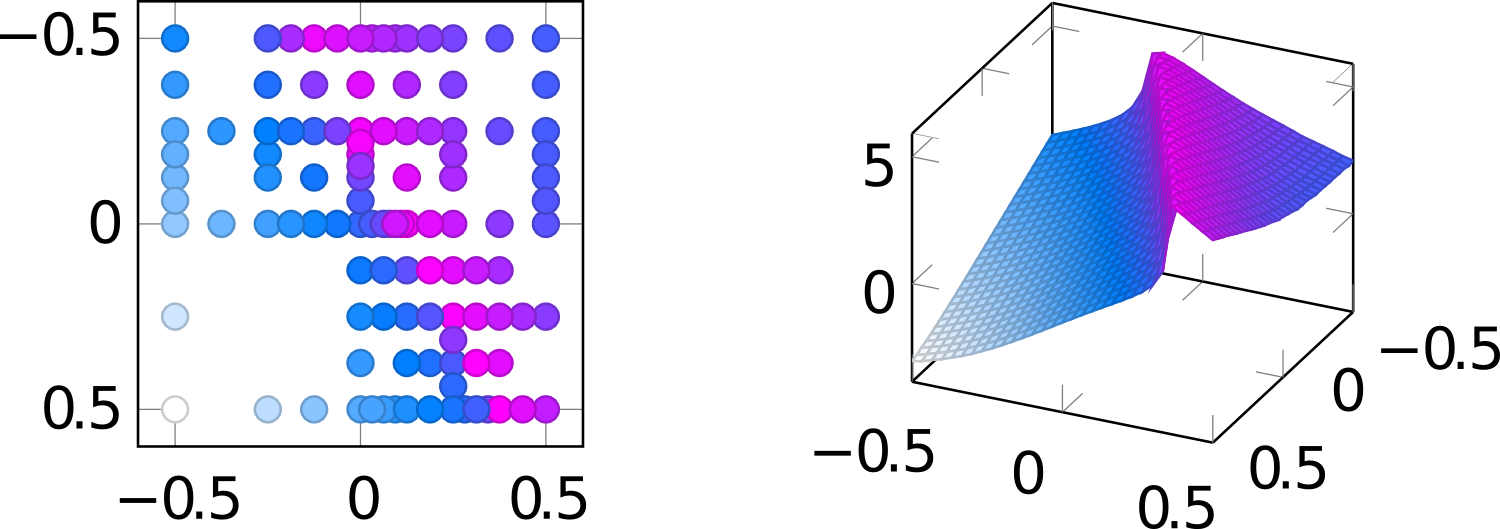
With significant errors in the rate parameters, local sensitivity analysis can only be the first step. For a more complete picture and to properly quantify the error propagation, global sensitivity analyses are needed. These generally require the numerical evalutaion of integrals over the parameter space. For this, we have implemented dimension and locally adaptive sparse grids based on locally supported basis functions. We have modified the original approach such that multi-processor enviroments can be better exploited for the simulation of the data. The above image shows the plane spanned by the first two parameters of the 22-parameter model for the CO oxidation on ruthenium dioxide. Left are the grid points in the plane and right the reaction rate.

Besides established models from classical catalysis for testing purposes, we investigate the photocatalytic CO₂ reduction on titania anatase. Together with colleagues from the Zuse Institute Berlin (C-SE6), we also consider this system to elucidate the effect of particle scale field heterogeneities on the intrinsic and particle averaged activity.

Publications

Döpking, S., Plaisance,C.P.,  Strobusch, D., Reuter, K. Scheurer, Ch. & Matera,S (2018). Addressing global uncertainty and sensitivity in first-principles based microkinetic models by an adaptive sparse grid approach, The Journal of Chemical Physics 148, 034102

Döpking, S., & Matera, S. (2017). Error propagation in first-principles kinetic Monte Carlo simulation. Chemical Physics Letters, 674, 28-32.

Hoffmann, M. J., Engelmann, F., & Matera, S. (2017). A practical approach to the sensitivity analysis for kinetic Monte Carlo simulation of heterogeneous catalysis. The Journal of Chemical Physics, 146(4), 044118

Gelß, P., Matera, S., Schütte, Ch. (2016). Solving the master equation without kinetic Monte Carlo: Tensor train approximations for a CO oxidation model. Journal of Computational Physics 314(1),  489-502

Matera, S., Maestri, M., Cuoci, A., & Reuter, K. (2014). Predictive-quality surface reaction chemistry in real reactor models: Integrating first-principles kinetic Monte Carlo simulations into computational fluid dynamics. ACS Catalysis, 4(11), 4081-4092.

Thesis

Döpking, S.  (2014).  Sensitivity analysis of the error propagation of first principles kinetic methods with a sparse grid approach. Master’s thesis, TU Munich

Engelmann, F. (2016). Linear Response and Sensitivity Analysis for kinetic Monte Carlo, Project report, TU Munich