PhD Theses
 Eric Zimmermann
Eric Zimmermann
Point Clouds - Between Local and Global Approaches.
PhD Thesis, Freie Universität Berlin, 2023
In this thesis we investigated set systems on geometric point data in Euclidean space from a macroscopic (first two chapters) and microscopic (last chapter) perspective.
In Chapter A we described cloud sets, which are set systems build on points which give rise to simplicial complexes as control structures. The preferred instance of such structure is a simplicial surface (making the cloud complex a cloud surface), so that the system of clouds mimics the properties of a collection of subsets we find in an atlas describing a 2-manifold. We discussed the generation of cloud surfaces on one hand starting with a simplicial surface, generating points, and placing them in clouds. On the other hand we focused on the reverse direction, obtaining the clouds from a point set which led to topolgical questions on coverings. In practice we used the cloud surfaces' underlying simplicial surface as a skeleton to perform point motions in Euclidean space.
In Chapter B we derived a second set system which is dual to the one in the first chapter under certain conditions. For the resulting complex we conjectured them to be surface-like, i.e. having combinatorial properties so that each point has at least an abstract vicinity which is perceivable to be 2-dimensional. For their construction we presented a k-means clustering approach for point sets coupled with an application of generating a simplified polygonal surface out of the segmentation also reconstructing polygonal faces which are not necessarily simply connected.
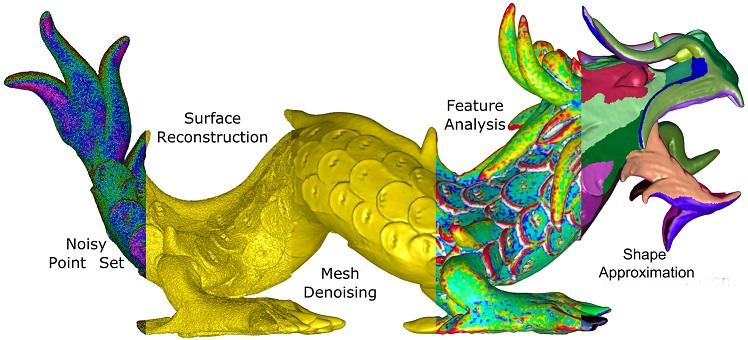
In Chapter C we partitioned the microscopic investigation inside a cloud in two. First we set up a large scale evaluation to determine a neighborhood around a point accounting as an approximation of a 2-dimensional vicinity using an energy model on feature classification entities built from eigenvalues obtained by a weighted point distribution analysis. The evaluation explores the parameter spaces of the weighting function and combinatorial neighborhood sizes of the point distributions. Secondly we proposed the flatness model as a feature classification entity favoring point distributions which appear to be 2-dimensional and not curve-like or volumetric. This continuous model then is incorporated into a point set denoising application to evaluate its potency using less parameters and preserving geometric features without the necessity of point normal information.
 Martin Skrodzki
Martin Skrodzki
Neighborhood Data Structures, Manifold Properties, and Processing of Point Set Surfaces. PhD Thesis, Freie Universität Berlin, 2019
The thesis covers three topics all centered in the context of point set processing. The first topic concerns notions of neighborhood and corresponding data structures. The second main topic of this thesis deals with manifold structures for point set surfaces. Third and finally, algorithms have to work efficiently and robustly on the point set. While meshed geometries provide an intuitive and natural weighting by the areas of the faces, point sets can at most work with distances between the points. This introduces a new level of difficulty to be overcome by any point set processing algorithm. This final chapter introduces a novel weighting scheme to counteract non-uniformity in point sets, a feature detection algorithm with mathematical guarantees, and an iterative denoising scheme for point sets.
 Sunil Kumar Yadav
Sunil Kumar Yadav
Surface Denoising based on The Variation of Normals and Retinal Shape Analysis. PhD Thesis, Freie Universität Berlin, 2018
Through the development of this thesis, starting from the curvature tensor, we have been able to understand the variation of tangent vectors to define a shape analysis operator and also a relationship between the classical shape operator and the curvature tensor on a triangular surface. In continuation, the first part of the thesis analyzed the variation of surface normals and introduced a shape analysis operator, which is further used for mesh and point set denoising. In the second part of the thesis, mathematical modeling and shape quantification algorithms are introduced for retinal shape analysis. In the first half, this thesis followed the concept of the variation of surface normals, which is termed as the normal voting tensor and derived a relation between the shape operator and the normal voting tensor. The concept of the directional and the mean curvatures is extended on the dual representation of a triangulated surface. A normal voting tensor is defined on each triangle of a geometry and termed as the element-based normal voting tensor (ENVT). Later, a deformation tensor is extracted from the ENVT and it consists of the anisotropy of a surface and the mean curvature vector is defined based on the ENVT deformation tensor. The ENVT-based mesh denoising algorithm is introduced, where the ENVT is used as a shape operator. A binary optimization technique is applied on the spectral components of the ENVT that helps the algorithm to retain sharp features in the concerned geometry and improves the convergence rate of the algorithm. Later, a stochastic analysis of the effect of noise on the triangular mesh based on the minimum edge length of the elements in the geometry is explained. It gives an upper bound to the noise standard deviation to have minimum probability for flipped element normals. The ENVT-based mesh denoising concept is extended for a point set denoising, where noisy vertex normals are filtered using the vertex-based NVT and the binary optimization. For vertex update stage in point set denoising, we added different constraints to the quadratic error metric based on features (edges and corners) or non-feature (planar) points. This thesis also investigated a robust statistics framework for face normal bilateral filtering and proposed a robust and high fidelity two-stage mesh denoising method using Tukey’s bi-weight function as a robust estimator, which stops the diffusion at sharp features and produces smooth umbilical regions. This algorithm introduced a novel vertex update scheme, which uses a differential coordinate-based Laplace operator along with an edge-face normal orthogonality constraint to produce a high-quality mesh without face normal flips and it also makes the algorithm more robust against high-intensity noise. The second half of thesis focused on the application of the proposed geometric processing algorithms on the OCT (optical coherence tomography) scan data for quantification of the human retinal shape. The retina is a part of the central nervous system and comprises a similar cellular composition as the brain. Therefore, many neurological disorders affect the retinal shape and these neuroinflammatory conditions are known to cause modifications to two important regions of the retina: the fovea and the optical nerve head (ONH). This thesis consists of an accurate and robust shape modeling of these regions to diagnose several neurological disorders by detecting the shape changes. For the fovea, a parametric modeling algorithm is introduced using Cubic Bezier and this algorithm derives several 3D shape parameters, which quantify the foveal shape with high accuracy. For the ONH, a 3D shape analysis algorithm is introduced to measure the shape variation regarding different neurological disorders. The proposed algorithm uses triangulated manifold surfaces of two different layers of the retina to derive several 3D shape parameters. The experimental results of the fovea and the ONH morphometry confirmed that these algorithms can provide an aid to diagnose several neurological disorders.
 Konstantin Poelke
Konstantin Poelke
Hodge-Type Decompositions for Piecewise Constant Vector Fields on Simplicial Surfaces and Solids with Boundary. PhD Thesis, Freie Universität Berlin, 2017
This dissertation develops a theory for Hodge-type decompositions of piecewise constant vector fields (PCVF) on simplicial surfaces and solids with boundary in R3 which is structurally consistent with the corresponding results in the smooth world. First, the necessary differential-geometric and topological foundations of Hodge decomposition statements on smooth manifolds with boundary are reviewed, with a particular focus on a recent result by Shonkwiler which classifies certain harmonic fields as cohomology representatives for either the cohomology induced by the boundary components, or the "inner topology" of the manifold. Next, based on linear Lagrange, Crouzeix-Raviart and Nédélec elements, a discrete Hodge-Morrey-Friedrichs decomposition for PCVFs on simplicial surfaces and solids with boundary is derived. Of particular importance are the spaces H_N and H_D of discrete harmonic Neumann and Dirichlet fields, respectively, as they represent certain cohomology classes of the manifold and are therefore deeply linked to the topology of the simplicial manifold.
For surfaces with boundary that come from a closed surface of genus g=0, one obtains a complete, L2-orthogonal five-term decomposition where both the spaces H_N and H_D appear as L2-orthogonal subspaces. On the other hand, if g>0, these two spaces are no longer orthogonal to each other, and there are now two orthogonal decompositions - one involving H_N, the other one involving H_D.
A deep result in the smooth world states that the spaces of Neumann and Dirichlet forms always have a trivial intersection, but the corresponding result for the discrete spaces does not hold in general.
Surprisingly, at this stage the combinatorics of the triangulating grid comes into play, and it becomes a matter of how the triangulation connects topologically rich regions with the boundary components to decide whether the statement holds true or not. Based on results by Lovász and Benjamini on weighted networks, a criterion is derived that guarantees the validity of the trivial-intersection result. Next, convergence of the derived decomposition statements is proved under the assumption that the simplicial geometry converges metrically against a smooth geometry. To this end, a seminal convergence result by Dodziuk on the approximation of smooth Hodge decomposition components by Whitney forms is generalized to include the refined discrete decompositions. One obtains convergence with respect to the L2-norm which is of linear order in the mesh size.
The dissertation concludes with two central applications of this discrete Hodge theory: the computation of harmonic cohomology representatives and the computational decomposition of a given PCVF.
For both applications, algorithms are presented and evaluated on various test models and the numerical aspects of the involved solving steps are discussed.
 Anna Wawrzinek
Anna Wawrzinek
On Isoparametric Catmull-Clark Finite Elements for Mean Curvature Flow. PhD Thesis, Freie Universität Berlin, 2016
In this thesis, we deal with the study of subdivision finite element methods for the solution of differential equations on curved surfaces based on the Catmull-Clark subdivisions. The focus is on quadrangular control grids and the characteristic parameterization of the limit surfaces. These are descried using the generalized B-spline basis functions of the Catmull-Clark type. In particular, we present a new finite element approach compatible with the classical definition of the subdivision surfaces. Compared to the previously used natural finite elements, the form of the grid and, consequently, the stability of the limit surface remains resistant. This is achieved as the characteristic finite elements inherit the continuity properties of the subdivision surfaces classically generated by grid refinements.
 Faniry H. Razafindrazaka
Faniry H. Razafindrazaka
Quad Layout Generation and Symmetric Tilings of Closed Surfaces. PhD Thesis, Freie Universität Berlin, 2016
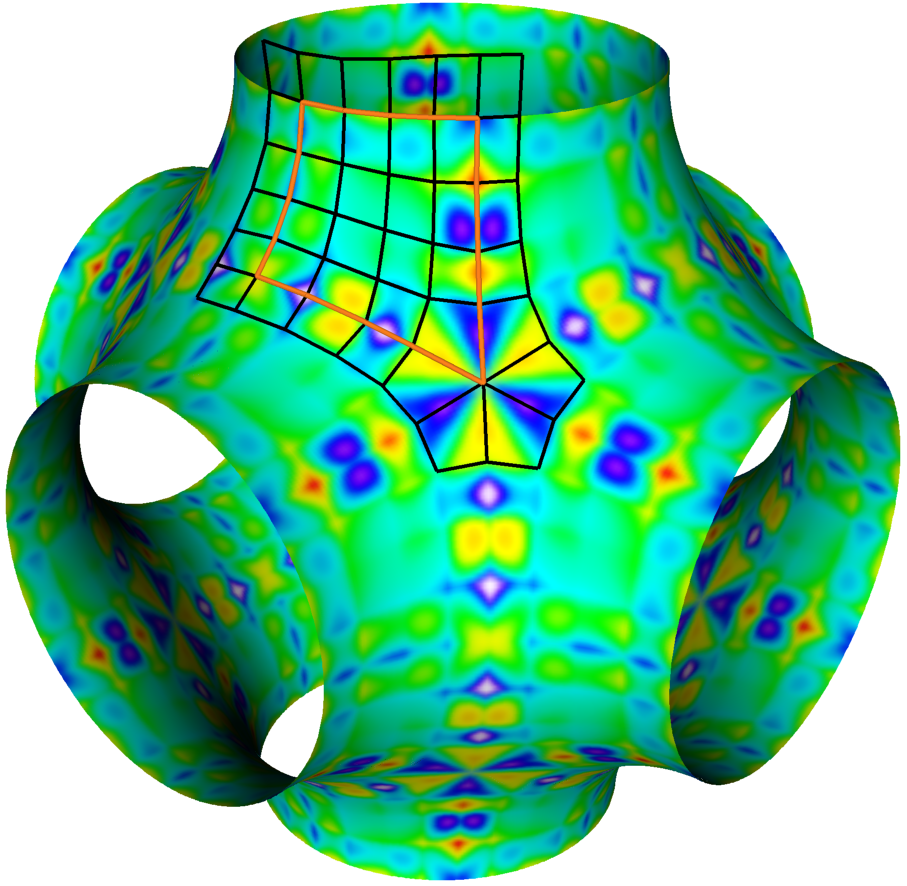
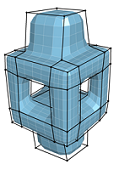
This thesis concerns two fundamental concepts in surface topology. The first part proposes a solution of the problem of generating an all quadrilateral patch layout on a given surface. We approach the problem from a combinatorial graph optimization point of view. Mainly, finding a nice quad layout of a given surface is equivalent to solving a minimum weight perfect matching problem with additional quad guarantee constraints. The results are of high quality in terms of coarseness and alignment to important features of the geometry which can be used for wide range of applications such as hierarchical subdivision or high order surface fitting. The second part suggests an algorithm to symmetrically generate high genus surfaces suitable for space models of regular maps. It is based on a novel identification in hyperbolic space to derive directly the tubular neighborhood of the edge of a tiling directly the the hyperbolic representation followed by a spring relaxation procedure with intersection-free guarantee. We succeed to produce new embeddings of regular maps ranging from genus 5 to 85.
 Maria Ella Kadas
Maria Ella Kadas
Methods to extract and quantify retinal Blood Vessels and Optic Nerve Head from optical Coherence Tomography Data in Neurological Disorders. PhD Thesis, Freie Universität Berlin, 2016
The eye’s retina is considered to be part of the central nervous system with similar structure and cellular composition like the brain. Thus, it has gained an important role in identifying structural changes that provide useful diagnostic information in many neurological disorders. Over the last decade, innovative advances in optical imaging technology have allowed us to identify these changes in the retinal architecture. Especially optical coherence tomography (OCT) has become a powerful imaging modality in ophthalmology and vision science. OCT non-invasively acquires in micrometer-resolution, three-dimensional (3D), cross-sectional images of biological tissues in vivo, producing in-depth views of the retina. With the 3D data sets, we can use 3D modeling and detection tools to allow more intuitive visualization and quantification of the structure in the data set, similar to the 3D tools created for magnetic resonance imaging or computed tomographic scans.
However, current OCT technology being mainly applied in the analysis and quantification of ophthalmological diseases lacks tailored image analysis methods for many changes caused by neurological disorders. The focus of this thesis lies on the development of segmentation and analysis methods to quantify two major components of the retina in confocal scanning laser ophthalmoscopy (cSLO data - 2D image) and in OCT data (3D OCT volume data), the retinal blood vessels, and the optic nerve head (ONH). The difficulty in developing robust and accurate methods for detecting these structures consists in the heterogeneous aspect of the data, coming from the natural anatomical diversity of the subjects, artifacts during data acquisition, especially in patients rather than in data from healthy control, and most importantly from certain structural changes that occur in the data during the disease course.
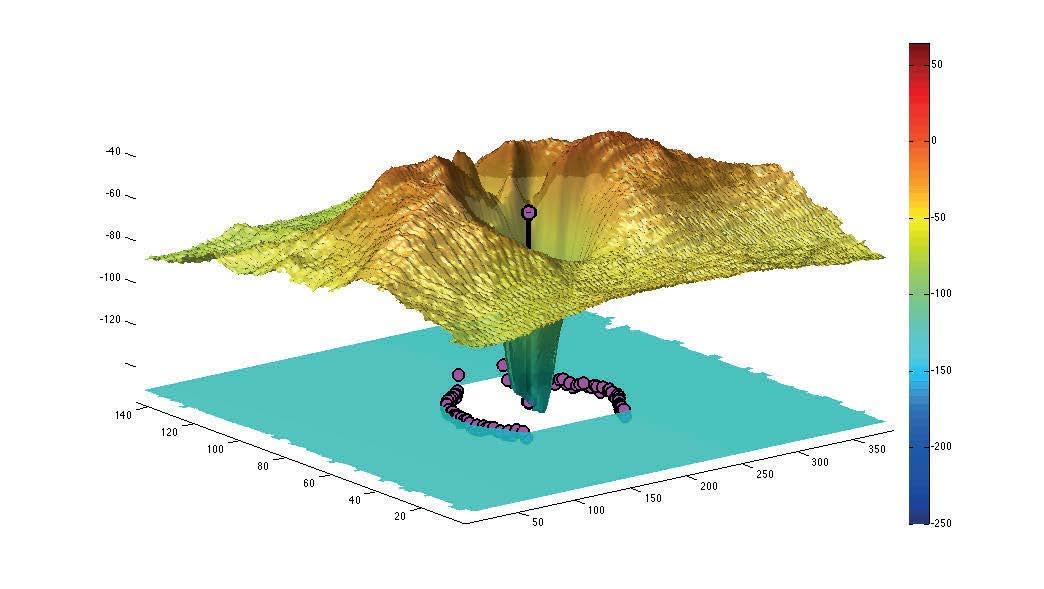
We present four approaches for extracting features from the retinal vasculature and for the ONH in multiple sclerosis (with its subtypes), neuromyelitis optica spectrum disorder and idiopathic intracranial hypertension. The first two approaches focus on the detection of the vasculature in SLO images. We propose a new 2D model of the vessel profile that accounts for the central reflex seen in this particular image type in order to quantify the vessel inner and outer boundary. Furthermore, we developed new filter response measures for vessel enhancement based on Morlet wavelet, the Hessian tensor, and an optimal oriented flux approach, and tested their capability of correctly detecting the vessel inner and outer boundary, curvature especially in junction regions. In the case of the ONH, we present a robust approach to detect a reference surface for the volume computation in atrophic and swelled ONH. Moreover, we present a novel algorithm for the detection of the ONH center directly in the 3D OCT volume. The basic idea of this method is to use the information from the computed reference surface to reduce the computation to a sub-volume (a reduced volume) in the ONH region. Furthermore, we address several challenges present in our data: motion artifacts due to eye/head movements by using a modified thin plate spline fitting that is able to model the natural curvature of the retina, artifacts arising from the shadows created by the presence of blood vessel by incorporating contextual textural features in a 3D grow-cut setting.
We evaluate our methods in various clinical settings. To demonstrate the effectiveness of our novel methods, we applied them to various patient and healthy control datasets.
 Christoph von Tycowicz
Christoph von Tycowicz
Concepts and Algorithms for the Deformation, Analysis, and Compression of Digital Shapes. PhD Thesis, Freie Universität Berlin, 2014
This thesis concerns model reduction techniques for the efficient numerical treatment of physical systems governing the deformation behavior of geometrically complex shapes. We present new strategies for the construction of simplified, low-dimensional models that capture the main features of the original complex system and are suitable for use in interactive computer graphics applications.
To demonstrate the effectiveness of the new techniques we propose frameworks for real-time simulation and interactive deformation-based modeling of elastic solids and shells and compare them to alternative approaches. In addition, we investigate differential operators that are derived from the physical models and hence can serve as alternatives to the Laplace-Beltrami operator for applications in modal shape analysis. Furthermore, this thesis addresses the compression of digital shapes. In particular, we present a lossless compression scheme that is adapted to the special characteristics of adaptively refined, hierarchical meshes.
 Stefan W. von Deylen
Stefan W. von Deylen
Numerical Approximation in Riemannian Manifolds by Karcher Means. PhD Thesis, Freie Universität Berlin, 2013
This dissertation treats questions about the definition of “simplices” inside Riemannian manifolds, the comparison between those simplices and Euclidean ones, as well as Galerkin methods for variational problems on manifolds. During the last three years, the “Riemannian centre of mass” technique introduced by Karcher (1977) has been successfully employed to define the notion of a simplex in a Riemannian manifold M of non-constant curvature by Rustamov (2010), Sander (2012) and others. This approach constructs, for given vertices p_i in M, a uniquely defined “barycentric map” x from the standard simplex Delta into the manifold, and calls x(Delta) the “Karcher simplex” with vertices pi. However, the question whether x is bijective and hence actually induces “barycentric coordinates” on x(Delta) remained open for most cases. We show that under “shape regularity” conditions similar to the Euclidean setting, the distortion induced by x is of the same order as for normal coordinates: dx is almost an isometry (of course, this can only work if Delta is endowed with an appropriately-chosen Euclidean metric), and "nabla dx" almost vanishes. The estimate on dx could have already been deduced from the work of Jost and Karcher (1982), but it is the combination with the "nabla dx" estimate which paves the ground for applications of Galerkin finite element techniques. For example, the construction can be employed to triangulate M and solve problems like the Poisson problem or the Hodge decomposition on the piecewise flat simplicial manifold instead of M. This leads to analogues of the classical estimates by Dziuk (1988) and subsequent authors in the field of surface pde’s (we only mention Hildebrandt et al. 2006 and Holst and Stern 2012 at this point), but as no embedding is needed in our approach, the range of the surface finite element method is extended to abstract Riemannian manifolds without modification of the computational scheme. Second, one can approximate submanifolds S inside spaces M unequal to R^m (for example, minimal submanifolds in hyperbolic space), for which the classical “normal height map” or “orthogonal projection” construction from the above-mentioned literature directly carries over, and the error term generated by the curvature of M is dominated by the well-known error from the principal curvatures of S. Apart from classical conforming Galerkin methods, there are other discretisation ideas, e. g. the “discrete exterior calculus” (DEC, see Hirani 2003) in which variational problems such as the Poisson problem or the Hodge decomposition can be solved without any reference to some smooth problem. Convergence proofs are less developed in this area, mainly because albeit there are interpolation operators from discrete k-forms to L^2 Omega^k, these interpolations do not commute with the (differing) notions of exterior derivative on both sides. We re-interpret DEC as non-conforming Galerkin schemes.
 Felix Kälberer
Felix Kälberer
Low Distortion Surface Parameterization. PhD Thesis, Freie Universität Berlin, 2013
This work deals with the parameterization of simplicial surfaces, that is, generation of a mapping between a surface and the Euclidean plane. Through this correspondence, the existing structure of the plane is transferable onto the surface. For example, the plane possesses a natural division into unit squares, and using the parameterization map one can transfer this structure onto the surface. Applications of this are, for example, remeshing and texturing of surfaces and the creation of control grids for subdivision or NURBS surfaces.
Parameterization maps usually have to meet a number of quality criteria, important examples are small angle and length distortion. In addition, it is often demanded that the gradient of the parameterization function are aligned with the direction of surface features such as sharp bends and edges.
Our QuadCover method, which forms the basis of this thesis, generates a parameterization automatically from a tensor field of feature directions. The method builds on the fact that such multi-dimensional direction fields can be interpreted as one-dimensional vector fields on a branched covering of the surface. In this way, known results about vector fields, such as Hodge decomposition, can be applied. On this basis, QuadCover finds a parameterization that aligns as close as possible to a given direction field.
Parameterizations of highest quality additionally require that length and angle distortion are minimized. For this, the number and location of branch points of the direction field is critical. In this work, we are pursuing several approaches: First, we show with a new method that the movement and especially the creation of branch points can drastically reduce distortion. Second, the distortion that is caused by the existence of branch points is reduced significantly by using a sophisticated rounding method. The third approach opposes the different types of distortion of the two former steps, and infers the optimal number of branch points out of them. The combination of the approaches makes it possible surpass even recent algorithms in terms of distortion.
 Christian Schulz
Christian Schulz
Interactive Spacetime Control of Deformable Objects and Modal Shape Analysis beyond Laplacian. PhD Thesis, Freie Universität Berlin, 2013
In der mathematischen Geometrieverarbeitung nutzt eine Vielzahl moderner und etablierter Methoden die Eigenschaften von Spektren und Eigenvektoren. So wurden unter anderem Verfahren zur Segmentierung, Parametrisierung und Deformation von Oberflächen entwickelt, die das Lösen generalisierter Eigenwertprobleme erfordern. In dieser Arbeit werden zwei Anwendungen vorgestellt, die von energiebasierten Spektren und Eigenfunktionen abhängen. Im Bereich der physikalisch basierten Computeranimation präsentieren wir eine Verallgemeinerung der üblichen Spline Interpolationsmethode von Keyframes. Unsere Verfahren ermöglicht die interaktive Kontrolle über eine Reihe von animationsrelavanten Parametern selbst für komplexe Formen, d.h. unter anderem für diskrete Geometrien die deformierbare Objekte, wie z.B. dünne Schalen oder elastische Körper, beschreiben. Die Interaktivität wird durch eine geeignete Problemreduktion und einer expliziten Darstellung der Wiggly Splines erreicht. Die Reduktion und die Darstellung der Wiggly Splines erfordert das Lösen generalisierter Eigenwertprobleme. Wir demonstrieren die Vielseitigkeit unseres Verfahrens an einer Reihe von Animationen für ein-, zwei- und dreidimensionalen Formen. Im Bereich der Oberflächenanalyse stellen wir eine neue Familie von Operatoren für Funktionen auf Oberflächen vor. Im Gegensatz zum Laplace- Operator besitzen diese Operatoren merkmals-sensitive Spektren und Eigenfunktionen. Wir konstruieren eine Punkt-Signatur, die auf den merkmalssensitiven Spektren und Eigenfunktionen basiert. Wir vergleichen die gefundenen ähnlichen Punkte bzgl. dieser Signatur mit Ergebnissen der Diffusionssignatur, d.h. einer Signatur die aus dem Laplacespektrum und Eigenfunktionen konstruiert wird. Weiterhin zeigen wir, dass das Spektrum eines bestimmten Operators dieser Familie zur Abschätzung des Stabilitätsindexes einer diskreten Fläche konstanter mittlerer Krümmung verwendet werden kann. Abschliessend stellen wir noch eine Methode vor, die eine merkmalssensitive Oberflächenstrukturierung ermöglicht.
 Klaus Hildebrandt
Klaus Hildebrandt
Discretization and Approximation of the Shape Operator, the Laplace--Beltrami Operator, and the Willmore Energy of Surfaces. PhD Thesis, Freie Universität Berlin, 2012
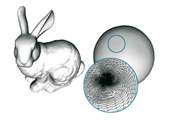
This thesis deals with discrete differential geometric properties of polyhedral surfaces in Euclidean 3-space. We develop a description of the curvatures of polyhedral surfaces based on a generalization of the shape operator, and we construct discretizations of the (strong form of the) Laplace-Beltrami operator and of the Willmore energy. The focus of our analysis is on approximation properties of the introduced discretizations. In particular, we show that the generalized shape operators can be used to approximate the classical shape operator of a smooth surface, and we prove the consistency of the discrete Laplace-Beltrami operators and the discrete Willmore energies. In addition, we consider a problem in geometry processing: the fairing of polyhedral surfaces. We develop a scheme for fairing under spatial constraints.
 Matthias Nieser
Matthias Nieser
Parameterization and Tiling of Polyhedral Surfaces. PhD Thesis, Freie Universität Berlin, 2012
The thesis addresses the problem of parameterizing simplicial surfaces, i.e. finding a map from the surface into the plane. The parameter lines should align to given frame fields, such as principal curvature directions on the surface.
Frame fields are multi-valued functions. In this thesis the equivalence of a frame field to a (single-valued) vector field on a Riemannian surface is shown. This observation lays the theoretical foundation for the QuadCover algorithm.
QuadCover automatically generates a global parameterization of an arbitrary two-dimensional polyhedral manifold. The resulting parameter lines form a mesh which is globally continuous and allows to remesh the surface into a mesh of high quality. The faces of the mesh consist of either quadrilaterals, triangles or hexagons.
Another application of QuadCover is texturing. The parameterization is used to cover the surface with an arbitrary tileable pattern. Thereby, the parameterization must be compatible with the rotational symmetry of the texture pattern. This thesis presents a method for tiling a surface with regular quadrilateral-, hexagonal-, triangular-, or stripe-patterns.
Often, a user has special demands on a parameterization which makes it necessary for the user to interact with the parameterization software. QuadCover allows to move singularities on the surface. Furthermore, the user can specify curves on the surface as geometric constraint, which means that a parameter line will exactly follow the given curve. There are also combinatorial constraints which allow to manipulate the topology of the generated mesh.
Max Wardetzky
Discrete Differential Operators on Polyhedral Surfaces - Convergence and Approximation. PhD Thesis, Freie Universität Berlin, 2006
This thesis studies discrete differential-geometric analogues of the smooth theory of two-dimensional Riemannian manifolds in the framework of discrete differential geometry (DDG). In particular, the following objects are considered on polyhedral surfaces: Laplace-Beltrami operator, gradient, divergence, curl, solutions to the Dirichlet problem, mean curvature vector, geodesics, complex structure, de Rham cohomology, Hodge decomposition, Hodge star operator, and spectrum of the Laplace operator. The discretization of these objects is primarily built upon the discretization of function spaces on polyhedra in the sense of linear finite elements. Accordingly, the first part of this thesis discusses weak derivatives and Sobolev spaces on polyhedral surfaces from which discrete differential complexes and their cohomological properties are derived. The second part deals with convergence and approximation properties of discrete differential operators. In particular, it is shown that the aforementioned (discrete) objects converge to their smooth counterparts if the points and normals of a sequence of polyhedral surfaces embedded into Euclidean 3-space converge to those of a smooth limit surface. A particular emphasis is put on the appropriate norms in which convergence can be expected. Several applications, specifically to computer graphics, are mentioned along the way.
