Abstract
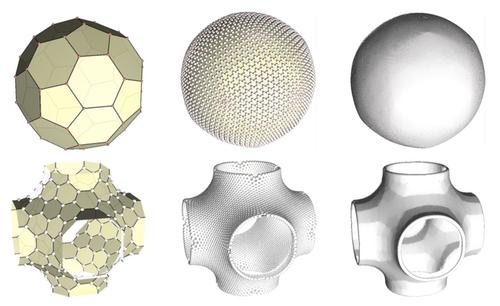
It is a fundamental problem in discrete geometry to find good discrete meshes approximating a given smooth surface. In this talk, however, we will investigate convergence in the opposite direction, namely, how to discover a converging subdivision process from a given discrete surface. 

We will consider trivalent graphs and their Goldberg-Coxeter subdivisions. Our aim is to find a proper smooth limit realization of such a subdivision sequence. In the present talk we will introduce three ways of smooth limit realizations and compare corresponding examples.

Biography
Tao Chen is a Ph.D student from Mathematical Institute of Tohoku University. He received the Bachelor of science in mathematics from Department of Mathematics, Beijing Institute of Technology, China and the Master of science in mathematics from Mathematical Institute, Tohoku University, Japan.

During the undergraduate period, he became interested in Riemannian Geometry and Information Geometry. His study on the principal bundle over statistical manifolds helps him to receive the Bachelor Degree. In 2014, he joined Kotani research group as a student and began the study of Discrete Differential Geometry. His research concentrates on building a convergence theory for discrete surfaces.