In order to avoid the curse of dimensionality, frequently encountered in Big Data analysis, there was a vast development in the field of linear and non-linear dimension reduction techniques in recent years. These techniques (sometimes referred to as manifold learning) assume that the scattered input data is lying on a lower dimensional manifold, thus the high dimensionality problem can be overcome by learning the lower dimensionality behavior. However, in real life applications, data is often very
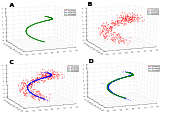
noisy. In this work, we propose a method to approximate a $d$-dimensional $C^{m+1}$ smooth submanifold $\mathcal{M}$ residing in $\mathbb{R}^n$ ($d << n$) based upon scattered data points (i.e., a data cloud). We assume that the data points are located ”near” a lower dimensional noisy manifold and perform a non-linear moving least squares projection. This method can also be used for approximating functions over the manifold. Under some mild assumptions, the resulting approximation to the manifold $\mathcal{M}$ is shown to be infinitely smooth and of approximation order of $O(h^{m+1})$ (where $h$ is the mesh size, and $m$ is the degree of the local polynomial approximation). Furthermore, the method presented here assumes no analytic knowledge of the approximated manifold and the approximation algorithm is linear in the large dimension $n$.