You are here: Foswiki>CompMolBio Web>DetailedBalance (03 Aug 2007, JanHendrikPrinz)Edit Attach

Page DetailedBalance

This is a discussion about the necessity of Detailed Balance in Markov Models

Definition

The probability of being in a state o at some time should be given by

\[p: (o,t) \longrightarrow p(o,t)\]

We define a probability flux from the old state ${}o$ to a new state ${}n$ during a fixed time step, which is a single time step in the underlying discrete Markov Model.

\[J: (o,n) \longrightarrow J(o,n)\]

We can then clearly express the change in the probabiliy during the unit timestep by

\[p(o,t+1) = p(o,t) + \sum\limits_n [J(n \rightarrow o) - J(o \rightarrow n)]\]

For the stationary distribution, we need

\[ p(o,t+1) = p(o,t)\]

to hold, which implies the sum to vanish identically. This means, that each state receives as much probability as it looses. In which way, does not matter.

One simple way to ensure this is to balance the flux between to states in both directions. This assumption is stronger than, what we wanted, but fulfills its purpose. This assumption is sufficient, but, and this is important!, not necessary and is referred to as Detailed Balance

\[J(n \rightarrow o) = J(o \rightarrow n) \]

The connection to Markov Models and Monte Carlo Simulation

Since with Monte Carlo Simulation the stress is on sampling the stationary distribution and not on the dynamics anymore. The idea is to explore the phase space in a somewhat random fashion and reject states during this exploration with the right probability, so that the remaining time series represents the stationary distribution.

This means, that in a MC algorithm a Probability Flux Matrix is constructed in such a way, that it will reproduce the right stationary distribution. To do this, the Flux from ${}o$ to ${}n$ is seperated in three parts, with the main idea to introduce a trial move probability and an acceptance probability
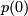  1. $p(0)$ the probability of being in state ${}o$
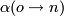  2. $\alpha(o \rightarrow n)$ the probability of generating a the trial move from ${}o$ to ${}n$
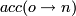  3. $acc(o \rightarrow n)$ the probability of accepting the trial move from ${}o$ to ${}n$

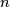
This gives finally

\[J(o \rightarrow n) = p(o) \times \alpha(o \rightarrow n) \times acc(o \rightarrow n)\]

For the probability of being in state o we use the stationary distribution, which is given by the model. Usually this is a Boltzmann Distribution with the energy from a given Potential Energy Landscape ${}U$. So this part is given.

The proposal step probability can be chosen arbitrarily, although one uses usually a symmetric one

\[\alpha(o \rightarrow n) = \alpha(n \rightarrow o)\]

Finally the detailed balance condition is used, to get information about the acceptance probability.

\[ \frac{acc(o \rightarrow n)}{acc(n \rightarrow o)} = \frac{\alpha(o \rightarrow n) p(n)}{\alpha(n \rightarrow o) p(o)} = \frac{\alpha(o \rightarrow n)}{\alpha(n \rightarrow o) }\times \exp(-\beta (U(n) - U(o)))\]

If now the proposal is symmetric we get for the acceptance

\[ acc(o \rightarrow n) = \min(1, \exp(-\beta (U(n) - U(o))))\]

This idea was first presented by N. Metropolis et al. J. Chem. Phys. 21, 1087 (1953)

In general all Monte Carlo Simulation use this trick, the difference is only in the proposal step, which is adapted to certain problems. The better or more intelligent the proposal step is, the higher the acceptance rate and the higher the rate of convergence of the time series to the stationary distribution.

Unfortunately one cannot proof that the simulation is ergodic. For this we need
  1. the simulation time to be long enough and
  2. the the proposed state to be statistically independant from the old state, which is
is general not fulfilled for Monte Carlo Simulations

In most cases this is sufficient, since the importants parts will be explored sooner or later, but one should think about the possibility, that even a simulation, that looks converge, has only explored a small part of the phase space. And one cannot give any information about parts, that have not even been discovered yet!

Comments

 
Edit  | Attach | Print version | History: r3 < r2 < r1 | Backlinks | View wiki text | Edit wiki text | More topic actions
Topic revision: r2 - 03 Aug 2007, JanHendrikPrinz
This site is powered by FoswikiCopyright © by the contributing authors. All material on this collaboration platform is the property of the contributing authors.
Ideas, requests, problems regarding Foswiki? Send feedback