When it comes to an interpretation of macroscopic reactivity in terms of atomistic driving forces, classical rate equation based approaches can provide only a limited insight. An alternative approach is to build the model 'bottom-up'. For this, predictive electronic structure methods are employed to derive a coarse-grained Markov model, which describes the statistical interplay of the elementary reaction events.

In the group, we develop tools for the simulation of such models with the kinetic Monte Carlo method (also termed Stochastic Simulation or dynamic Monte Carlo). In particular, we focus on problems, which can be mapped on a lattice representation, and are co-developing the kmos software package. Typical problems, which can be treated which such models, are heterogeneous catalysis (also photo-catalysis), crystal growth or ion transport in batteries. But also electron/hole transport can often be mapped on a lattice model.

Tensor network approximation for the solution of the master equation

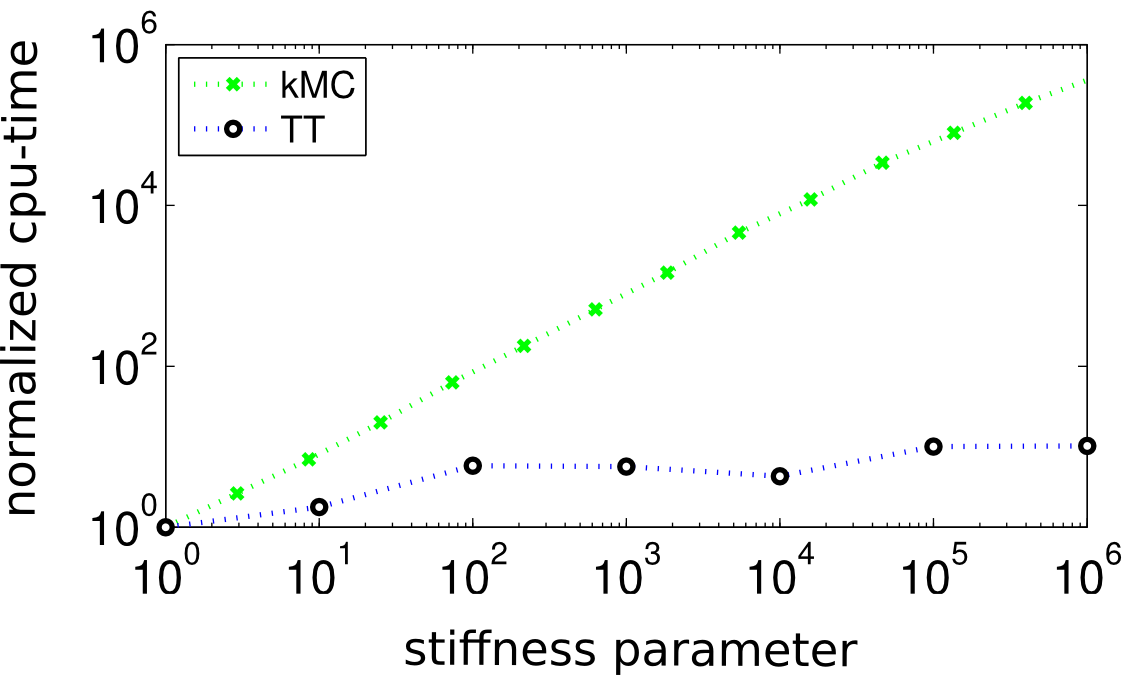
Kinetic Monte Carlo simulations become inefficient, when the Markov model becomes stiff. In this case, the simulations will require many steps to reach reasonable times. We therefore seek for a direct solution of the corresponding master equation using implicit differential equation integrators. Classical numerical approaches for solving the linear sub-problems suffer from high dimensionality (> 10¹⁰⁰ unknown are easily reached). We address this problem by employing tensor-network approximations, which have the potential to break curse of dimensionality. Up to now, our developments concentrate on the Tensor Train format and we have able to obtain linear cpu-time scaling with system size while being hardly affected by the stiffness, at least for the problems we have been testing so far. The above image compares the behaviour of the cpu-time for Tensor Trains and kinetic Monte Carlo for increasing stiffnenss.

Publications

Gelß, P., Klus, S., Matera, S., & Schütte, C. (2017). Nearest-neighbor interaction systems in the tensor-train format. Journal of Computational Physics, 341, 140-162.

Lorenzi, J.M., Matera, S. , & Reuter, K., Synergistic inhibition of oxide formation in oxidation catalysis: A first-principles kinetic Monte Carlo study of NO+CO oxidation at Pd(100) (submitted)

Gelß, P., Matera, S., & Schütte, Ch. (2016). Solving the master equation without kinetic Monte Carlo: Tensor train approximations for a CO oxidation model. Journal of Computational Physics 314(1),  489-502

Hoffmann, M. J., Matera, S., & Reuter, K. (2014). kmos: a lattice kinetic Monte Carlo framework. Computer Physics Communications, 185(7), 2138-2150.

Blomberg, S., Hoffmann, M. J., ..., S. Matera, ... & Lundgren, E. (2013). In situ x-ray photoelectron spectroscopy of model catalysts: At the edge of the gap. Physical review letters, 110(11), 117601.

Matera, S., Meskine, H., & Reuter, K. (2011). Adlayer inhomogeneity without lateral interactions: Rationalizing correlation effects in CO oxidation at RuO2 (110) with first-principles kinetic Monte Carlo. The Journal of chemical physics, 134(6), 064713.

Meskine, H., Matera, S., Scheffler, M., Reuter, K., & Metiu, H. (2009). Examination of the concept of degree of rate control by first-principles kinetic Monte Carlo simulations. Surface Science, 603(10), 1724-1730.