Multilevel adaptive sparse grids for parametric stochastic simulation models of charge transport 

Project Head: Sebastian Matera

Research Staff: Sandra Döpking

Funding: This research is carried out in the framework of Matheon supported by Einstein Foundation Berlin

Internal cooperation: M. Liero, A. Glitzky (WIAS), B. Schmidt, R. Klein (FU)

External cooperation: Ch. Scheurer (TUM),

---

Background

Many computational approaches utilize some kind of statistical sampling in order to address  the high-dimensional nature of the underlying model. Prototypical examples are Monte Carlo integration, Molecular Dynamics or Stochastic Simulation (kinetic Monte Carlo). By their stochastic nature, the estimated expectations contain some noise, which variance depends on the invested compuational resources.Besides this stochastic simulation noise, we have an additional source of error due to the limited accuracy of the input parameters of the model, such as interaction parameters for Molecular Dynamics or rate parameters for a Stochastic Simulation.

In project SE23, we develop a multilevel adaptive sparse grid approach to address the parametric uncertainty of such stochastic computational models. The idea is to exploit the intrisic multi-level structure of the sparse grids and to reduce the sampling accuracy of the model evaluations, when the grid gets refined. This is balanced such that the refinement criterion can be estimated with some given accuracy and the grid refinement strategy is likely to produce the same mesh as if the data would contain no noise.

This strategy is going to be applied to models describing charge transport, which is an important  aspect of in many sustainable energy applications such as solar cells, batteries or (artificial) photosynthesis.

Results

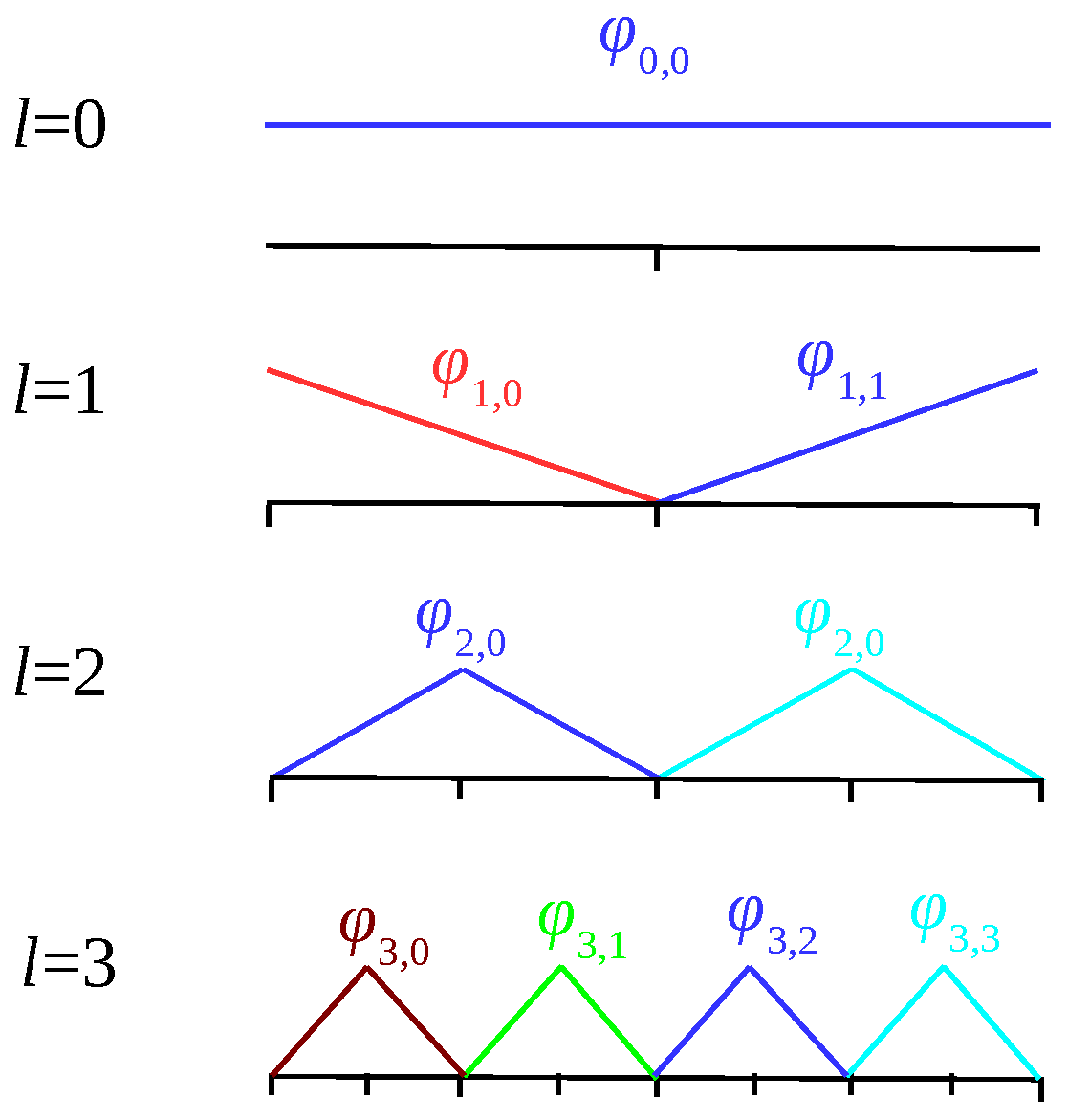
Sparse grids are based on products of one-dimensional basis functions. We employ a hierarchical basis {b_l,i} for piecewise linear interpolation, which is shown in the above figure for the levels l=0-3. From this, the d-dimensional basis functions {b_l,i} are created and we approximate the function of interest by

        f(x)≈f_L(x)=Σ_l,i a_l,i b_l,i (x)

Refinement is governed by hierarchical surplus {a_l,i}  times the integration weight {w_l,i} of the basis functions, i.e. we refine if

        a_l,i w_l,i > tol

where tol is a user defined threshold.

Now, by the Monte Carlo method which we use to evaluate f(x), the surpluss {a_l,i} will carry a random error and if this is too large the refinement will become also random. Thus the sampling error of the surpluss must be controlled such that accidental false refinement (or non-refinement) becomes unlikely. Since the weights decay as 2^-|l|₁, we can  increase the sampling variance for the new grid points in each level, while the probability for false refinement decisions remains approximately the same.

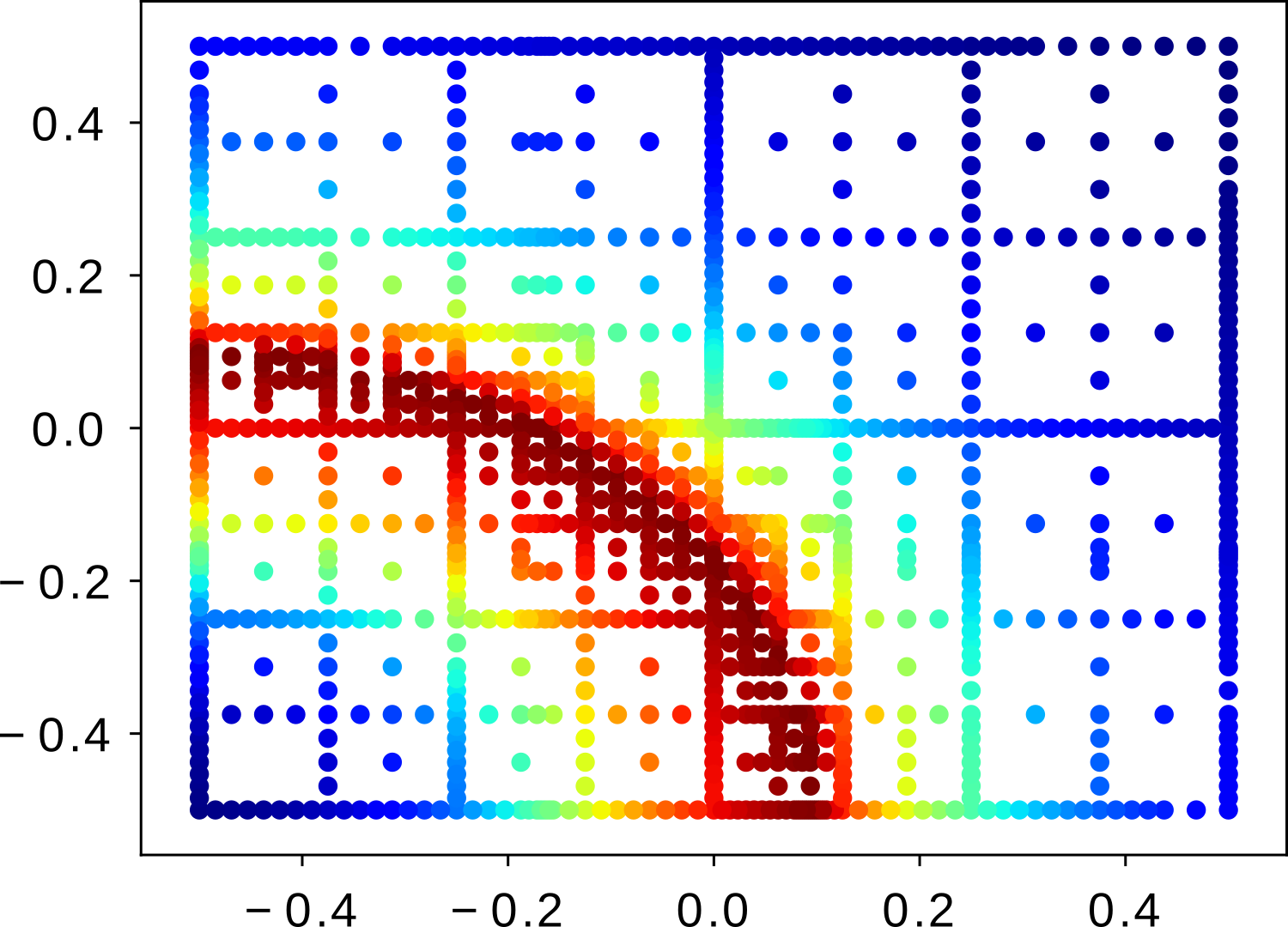
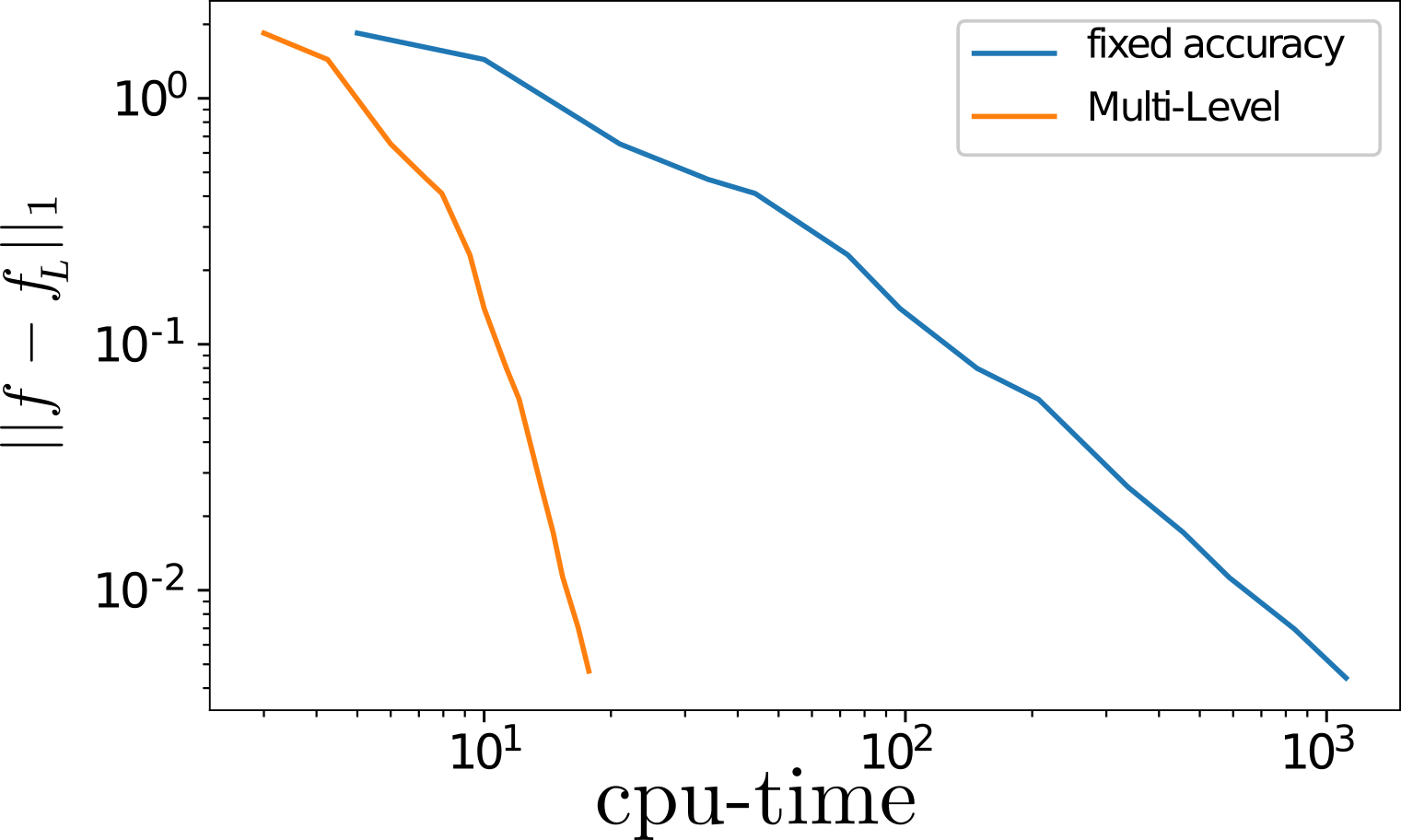
The above image shows the adaptive grid resulting from the multi-level strategy for a test function, where we added gaussian white noise onto the function value to mimic the simulation output.  The below image shows the decay of the 1-norm approximation error with the (virtual) cpu-time for the function evaluations, assuming that the variance of the simulation noise decays inversely proportional with the cpu-time. The multilevel strategy is displayed as orange line. For comparison, we have added the single level strategy where all data is estimated with the same accuracy (blue).

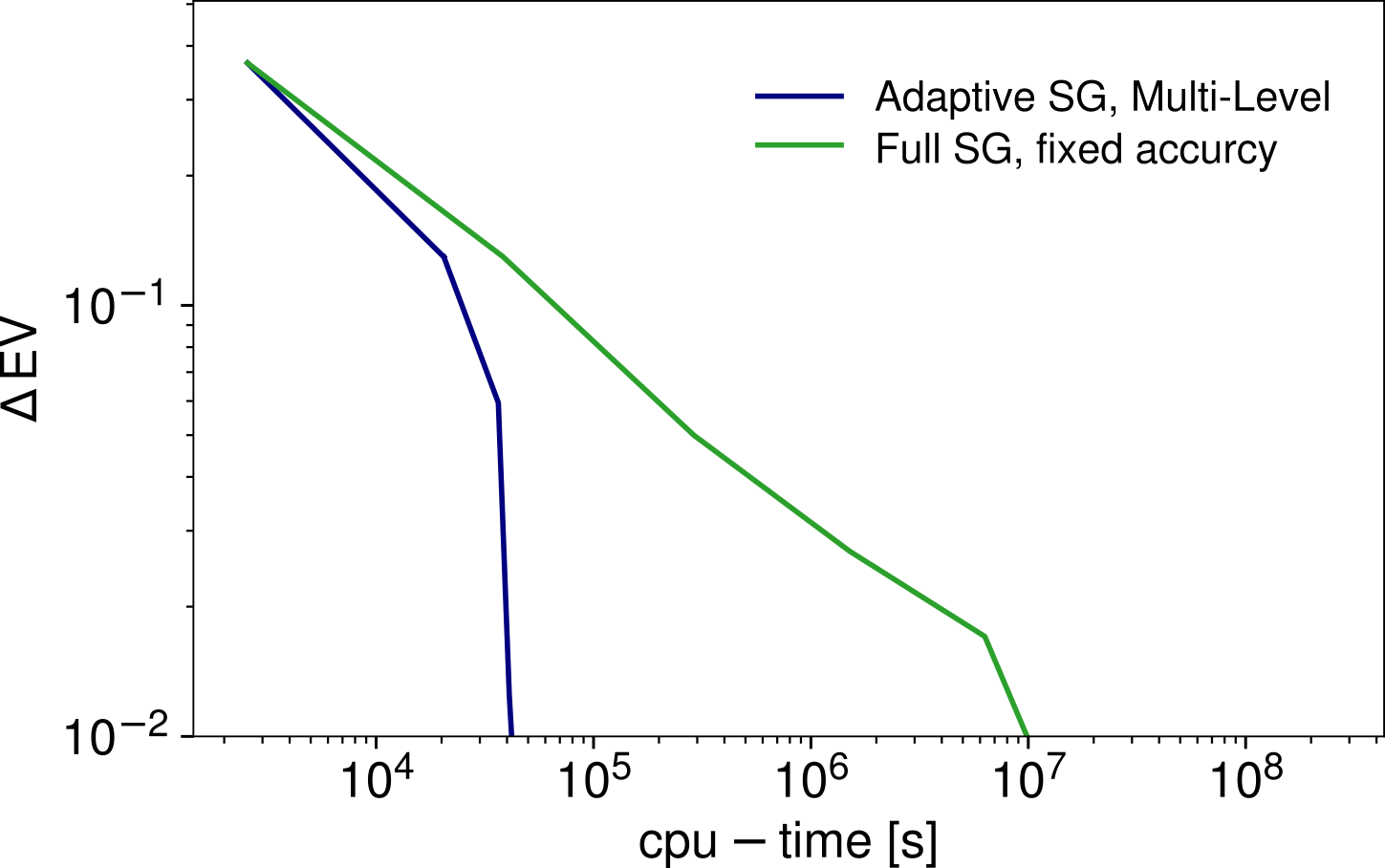
The image below shows the results for a kinetic Monte Carlo model from the field of heterogenous catalysis. This model depends on seven parameters and the integration domain has been chosen such that the function of interest has rapid decay from 1 to 0 in a narrow transition region which cuts the domain into two halfs of roughly the same volume. Shown is the error in the expected value assuming uniformly distributed parameters and comparing multi-level adaptive sparse grids with nonadaptive sparse grids with a fixed sampling accuracy.