Sensititivy Analysis in the Degenerate Case for Perron-Eigenvalues

We use a paper from N. Singhal and V. Pande as reference and start from there. We proceed in analogy to appendix B. We extend the Sensitivity Analysis for the case, that an eigenvalue is degenerate. Since we are interested in the computation of the stationary distribution of a system, which has been sampled by short trajectories. This can lead to transition matrices, which do not have one unique Perron-Eigenvector, but a few, which correspond to completely seperated subspaces. In particular this can happen, when the trajectory is started in state, that are known to exist, but have not been observed by previous trajectories. We will concentrate only on the case, where the eigenvector subspace to the eigenvalue one is degenerated. In this particular case a few step even simplify.

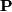
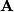
To compute the stationary distribution we need to compute the left eigenvalues of to the eigenvalue one or of to the eigenvalue zero, which is equivalent to find a basis for the kernel or the nullspace. To compute left eigenvalues, with an algorithmus written for right eigenvalues, one needs to transpose the matrix in question and proceed as usual.

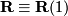
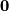
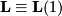
We start with an eigenvector equation, where is the Matrix of right eigenvectors (in columns) to the eigenvalue one and the is a zeromatrix of the same size. In analogy is the matrix of left eigenvectors (in rows).

Since we are looking at statistical matrices, we know, that the right PerronEigenvectors are constant on a seperated subspace, so if we choose the right eigenvectors to be orthogonal, these are zero everywhere execept on the indices referring to a state in a certain subspace. These indices are constant and we will choose these to be equal to one.

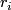
So now we have split the matrix in several subspaces indicated by the characteristic vectors . The left eigenvectors indicate now the stationary distribution inside one of these subspaces. To proceed, we need to choose a basis of left eigenvectors, so that these are also confined to the subspaces. We express this by

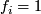
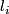
Finally we choose the , so that the stationary distribution in one subspace is given by . This is equal to

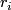
and is different to (B4), where the euklidian norm is chosen. We assume explicitly for the sensitivity, that the subspaces will be kept and not, that the degeneracy is destroyed. Meaning, that the are constant

This leads to a form for equation (B6)

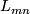
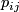
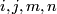
For computational reasons we only need to compute the entries of the variation of to , when are in the same subspace, otherwise the value is zero. At least I think, I have to check that. At least I assume, when the degeneracy is maintained.