Background

In optimal control and variational data assimilation problems with nonlinear time-dependent 3D PDEs, the storage of a full 4D discretization is usually prohibitive. For this reason gradient and quasi-Newton methods working on the reduced functional are often employed. The computation of the reduced gradient by adjoint methods requires one forward (in time) solve of the state equation and one backward solve of the adjoint equation. The state enters into the adjoint equation, such that the state tra jectory needs to be stored, again incurring the storage requirement of a full 4D discretization. 

So-called checkpointing techniques have been developed to reduce the storage requirement. The state is stored only at selected time points, from where on short parts of the state trajectory can be recomputed. Sophisticated choice of checkpoints and dynamic reuse of storage results in drastic reductions of storage requirements at the cost of a moderate increase in computing time. From a predictive coding point of view, checkpointing is a lossless compression scheme with an exact but expensive predictor. For this reason, no predictor errors need to be coded. 

The aim of this project is to investigate the potential benefit of using inexact but cheap predictors with additional coding of the prediction errors for solving the impulse thermography problem. Since the data is to be used inside a discretized, iterative algorithm, lossy coding is sufficient

Trajectory Compression

For the compression algorithm, three main ingredients are used: prediction, quantization of prediction errors, and entropy coding. First,  an approximation to the finite element solution of the state equation at the current time step is constructed. An inexact predictor is used to achieve a reasonable cheap computational complexity. Spatial correlations are exploited using prolongation in mesh hierarchies, while temporal correlations are exploited by differential encoding. As the adjoint equation is integrated backwards in time, no random access is necessary. Uniform quantization of the prediction error, and entropy coding of the quantized values reduces the storage requirement at the price of a loss of information.

The pictures above show a reconstructed solution at a given timestep for a semilinear equation. For the left picture, a maximal quantization error of 0.005 was allowed, leading to a storage requirement of 0.84 bits/vertex. The tolerance for the right picture was 0.05, resulting in 0.25 bits/vertex.

During an iterative optimization scheme, the quantization error tolerance can be chosen adaptively depending on the gradient norm to ensure convergence.

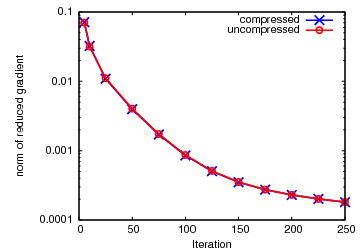
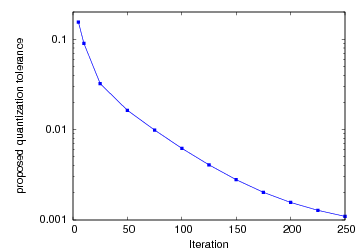
The plots above show the optimization progress and the proposed quantization tolerance for a linear boundary control problem. The convergence behavior is the same for lossy compressed and uncompressed storage. Compression factors range between more than 400 in the beginning to 40 in the final steps of the optimization algorithm.

Mesh Compression

For the compression of the underlying adaptive multi-resolution meshes, a lossless connectivity compression scheme that exploits the parent-child relationships inherent to the mesh hierarchy was developed. The tree-like hierarchical structure is converted to a binary stream, using the refinement scheme's rules to prune redundant bits. With context-based arithmetic coding and an adapted traversal of the mesh, taking advantage of structural regularities leads to compression ratios which exceed that of state-of-the-art coders by factors of 2 to 7. Sequences of meshes with varying refinement can be compressed exploiting temporal coherence.

For efficient compression of vertex positions and state values, popular wavelet-based coding schemes were adapted to the adaptive cases. Akin to state-of-the-art coders, a zerotree is used to encode the resulting coefficients. Using improved context modeling, the overall geometry data rate was reduced by 7% below those of the successful Progressive
Geometry Compression. More importantly, by exploiting the existing refinement structure, compression factors that are 4 times greater than those of coders that can handle irregular meshes are achieved.

Software

The trajectory compression has been implemented in Kaskade 7, a flexible C++ toolbox for solving PDE problems. The mesh compression has been implemented in JavaView, an interactive Java code for mathematical geometry processing and visualization. Both packages have been combined via the Java Native Interface to allow a fully adaptive solution of optimal control problems with compression of both, solution data and meshes.